March 25, 2009 feature
Spacetime May Have Fractal Properties on a Quantum Scale
(PhysOrg.com) -- Usually, we think of spacetime as being four-dimensional, with three dimensions of space and one dimension of time. However, this Euclidean perspective is just one of many possible multi-dimensional varieties of spacetime. For instance, string theory predicts the existence of extra dimensions - six, seven, even 20 or more. As physicists often explain, it’s impossible to visualize these extra dimensions; they exist primarily to satisfy mathematical equations.
As if extra dimensions weren’t strange enough, new research has probed an even more mind-bending possibility: that spacetime has dimensions that change depending on the scale, and the dimensions could have fractal properties on small scales. In a recent study, Dario Benedetti, a physicist at the Perimeter Institute for Theoretical Physics in Waterloo, Ontario, has investigated two possible examples of spacetime with scale-dependent dimensions deviating from classical values at short scales. More than being just an interesting idea, this phenomenon might provide insight into a quantum theory of relativity, which also has been suggested to have scale-dependent dimensions. Benedetti’s study is published in a recent issue of Physical Review Letters.
“It is an old idea in quantum gravity that at short scales spacetime might appear foamy, fuzzy, fractal or similar,” Benedetti told PhysOrg.com. “In my work, I suggest that quantum groups are a valid candidate for the description of such a quantum spacetime. Furthermore, computing the spectral dimension, I provide for the first time a link between quantum groups/noncommutative geometries and apparently unrelated approaches to quantum gravity, such as Causal Dynamical Triangulations and Exact Renormalization Group. And establishing links between different topics is often one of the best ways we have to understand such topics.”
In his study, Benedetti explains that a spacetime with quantum group symmetry has in general a scale-dependent dimension. Unlike classical groups, which act on commutative spaces, quantum groups act on nocommutative spaces (e.g. where xy doesn’t equal yx), which emerges through their unique curvature and quantum uncertainty. Here, Benedetti considers two types of spacetime with quantum group symmetry - a quantum sphere and k-Minkowski spacetime - and calculates their dimensions. In both spaces, the dimensions have fractal properties at small scales, and only reach classical values at large scales.
“In simple words, the relation between quantum groups and noncommutative geometry is as follows,” he explained. “Classically, we know that certain spaces are invariant under the action of some classical groups; for example, Euclidean space is invariant under rotations and translations. A quantum group is a deformation of a given classical group, and is such that no classical space can have it as a symmetry group. The invariant space has to be as well a deformation of a classical space, a deformation that makes it noncommutative. No relation of all this to fractals is known, but in my work I've found that they do have a common property, that is, a non-integer dimension (at some scale).”
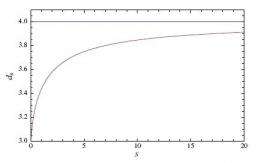
Compared to a Euclidean sphere, a quantum sphere’s curvature and uncertainty make it a noncommutative space. When calculating the spectral dimension of the quantum sphere, Benedetti found that it closely resembles a standard sphere on large scales; however, as the scale decreases, the dimensions of the quantum sphere deviate and go down to zero. He describes this phenomenon as a signature of the fuzziness, or uncertainty, of the quantum sphere, and also as resulting from fractal behavior at small scales.
In the second kind of space, k-Minkowski spacetime, the dimensions also deviate from the constant behavior of classical Minkowski spacetime. While the latter always has four dimensions, independent of the scale, the number of dimensions in the quantum version decreases to three as a function of the scale. In both k-Minkowski spacetime and the quantum sphere, the dimensionality becomes non-integral, which is a typical signature of fractal geometry.
Benedetti’s results match previous approaches to quantum gravity, which also point to the emergence of a ground-scale spacetime with fractal properties. Together, these studies may help scientists understand the unique Planck scale properties of spacetime, and possibly tie in to a quantum theory of gravity. For instance, as Benedetti explains, the fractal nature of quantum spacetime might enable gravity to cure its own ultraviolet behavior by dimensional reduction.
“The main problem with gravity is that apparently it cannot be quantized as other field theories; in jargon it is said to be non-renormalizable,” he said. “This problem is specific to four-dimensional spacetime. If spacetime had only two dimensions, then quantum gravity would be much simpler and treatable. The problem with a two-dimensional theory is that it is unphysical, as we see four dimensions at our scales. Things can be solved combining four and two dimensions at different scales. That is, if gravity itself provides a mechanism by which the dimension of spacetime depends on the scale at which we probe it (four at our and larger scales and two at very short scales), then we could have a physical theory (compatible with observations) that is free of quantum (short scale) troubles.”
More information: Benedetti, Dario. “Fractal Properties of Quantum Spacetime.” Physical Review Letters 102, 111303 (2009).
Copyright 2009 PhysOrg.com.
All rights reserved. This material may not be published, broadcast, rewritten or redistributed in whole or part without the express written permission of PhysOrg.com.