The new shape of music: Music has its own geometry, researchers find
The connection between music and mathematics has fascinated scholars for centuries. More than 200 years ago Pythagoras reportedly discovered that pleasing musical intervals could be described using simple ratios.
And the so-called musica universalis or "music of the spheres" emerged in the Middle Ages as the philosophical idea that the proportions in the movements of the celestial bodies -- the sun, moon and planets -- could be viewed as a form of music, inaudible but perfectly harmonious.
Now, three music professors – Clifton Callender at Florida State University, Ian Quinn at Yale University and Dmitri Tymoczko at Princeton University -- have devised a new way of analyzing and categorizing music that takes advantage of the deep, complex mathematics they see enmeshed in its very fabric.
Writing in the April 18 issue of Science, the trio has outlined a method called "geometrical music theory" that translates the language of musical theory into that of contemporary geometry. They take sequences of notes, like chords, rhythms and scales, and categorize them so they can be grouped into "families." They have found a way to assign mathematical structure to these families, so they can then be represented by points in complex geometrical spaces, much the way "x" and "y" coordinates, in the simpler system of high school algebra, correspond to points on a two-dimensional plane.
Different types of categorization produce different geometrical spaces, and reflect the different ways in which musicians over the centuries have understood music. This achievement, they expect, will allow researchers to analyze and understand music in much deeper and more satisfying ways.
The work represents a significant departure from other attempts to quantify music, according to Rachel Wells Hall of the Department of Mathematics and Computer Science at St. Joseph's University in Philadelphia. In an accompanying essay, she writes that their effort, "stands out both for the breadth of its musical implications and the depth of its mathematical content."
The method, according to its authors, allows them to analyze and compare many kinds of Western (and perhaps some non-Western) music. (The method focuses on Western-style music because concepts like "chord" are not universal in all styles.) It also incorporates many past schemes by music theorists to render music into mathematical form.
"The music of the spheres isn't really a metaphor -- some musical spaces really are spheres," said Tymoczko, an assistant professor of music at Princeton. "The whole point of making these geometric spaces is that, at the end of the day, it helps you understand music better. Having a powerful set of tools for conceptualizing music allows you to do all sorts of things you hadn't done before."
Like what?
"You could create new kinds of musical instruments or new kinds of toys," he said. "You could create new kinds of visualization tools -- imagine going to a classical music concert where the music was being translated visually. We could change the way we educate musicians. There are lots of practical consequences that could follow from these ideas."
"But to me," Tymoczko added, "the most satisfying aspect of this research is that we can now see that there is a logical structure linking many, many different musical concepts. To some extent, we can represent the history of music as a long process of exploring different symmetries and different geometries."
Understanding music, the authors write, is a process of discarding information. For instance, suppose a musician plays middle "C" on a piano, followed by the note "E" above that and the note "G" above that. Musicians have many different terms to describe this sequence of events, such as "an ascending C major arpeggio," "a C major chord," or "a major chord." The authors provide a unified mathematical framework for relating these different descriptions of the same musical event.
The trio describes five different ways of categorizing collections of notes that are similar, but not identical. They refer to these musical resemblances as the "OPTIC symmetries," with each letter of the word "OPTIC" representing a different way of ignoring musical information -- for instance, what octave the notes are in, their order, or how many times each note is repeated. The authors show that five symmetries can be combined with each other to produce a cornucopia of different musical concepts, some of which are familiar and some of which are novel.
In this way, the musicians are able to reduce musical works to their mathematical essence.
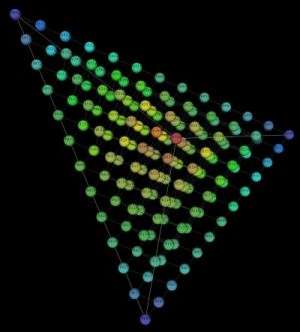
Once notes are translated into numbers and then translated again into the language of geometry the result is a rich menagerie of geometrical spaces, each inhabited by a different species of geometrical object. After all the mathematics is done, three-note chords end up on a triangular donut while chord types perch on the surface of a cone.
The broad effort follows upon earlier work by Tymoczko in which he developed geometric models for selected musical objects.
The method could help answer whether there are new scales and chords that exist but have yet to be discovered.
"Have Western composers already discovered the essential and most important musical objects?" Tymoczko asked. "If so, then Western music is more than just an arbitrary set of conventions. It may be that the basic objects of Western music are fantastically special, in which case it would be quite difficult to find alternatives to broadly traditional methods of musical organization."
The tools for analysis also offer the exciting possibility of investigating the differences between musical styles.
"Our methods are not so great at distinguishing Aerosmith from the Rolling Stones," Tymoczko said. "But they might allow you to visualize some of the differences between John Lennon and Paul McCartney. And they certainly help you understand more deeply how classical music relates to rock or is different from atonal music."
Source: Princeton University