Materials scientists and mathematicians benefit from newly crafted polymers

For the first time, the synthesis of a multicyclic type of polymer provides insights for tailoring polymer properties as well as the mathematics of complex geometries.

Polymers come with a range of properties dictated by their chemical compositions and geometrical arrangement. A team of researchers at Tokyo Institute of Technology have now applied an approach to synthesise a new type of multicyclic polymer geometry. "This additional step will give a library of architectures to allow systematic studies of what properties derive from what structures," explains Yasuyuki Tezuka, adding, "Mathematicians who study these complex geometries are also interested to know they can be made at the nanoscale."

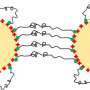
Rings have very different properties to linear polymers,particularly when considering dynamic rather than static characteristics, such as diffusion. Tezuka adds that these differences are amplified when moving from single ring or linear chains to self-assembled structures such as micelles—pompom-ball-like structures of aggregated linear chains.

However, the Tokyo Tech researchers were motivated more by the geometry itself than the possible applications. While mathematicians are interested because these structures are novel, the geometry studies also provide insights for chemists. "You may have two complex structures that are so-called isomers, that is, they are from identical starting materials like brothers," explains Tezuka. "The geometry tells us that the two constructions are isomers."

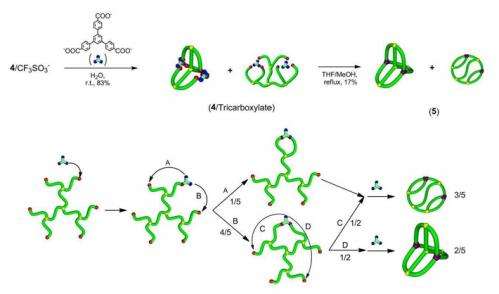
In fact, the geometry of the polymer, known as K_3,3, has been a popular field of study for mathematicians in graph theory. The geometry comprises four rings (tetracyclic) fused three ways (triply fused) with an inherently non-planar structure.

The team's approach combines fixation by covalent bonding with electrostatic self-assembly, which involves negatively and positively charged molecular units coming together, as in a salt. Salts should be insoluble in organic solvents, "But in polymer synthesis the situation is different," explains Tezuka. "The polymer is a long chain, and very hydrophobic and organically soluble. So if you add a little salt it is still soluble."

While a number of multicyclic polymers have been achieved using this approach since it was developed by Tezuka and his colleagues ten years ago, it is not so easy when several charged units are involved. The team succeeded by developing special highly branched and symmetric molecular chemicals and adding ionic groups and polymer chain ends. "The result came from trial and error and then we optimised the chemistry," says Tezuka.

He emphasises the contribution of a particularly dedicated student, Takuya Suzuki, who successfully exploited the difference in size of the component molecules to separate the two final products of these reactions: the non-planar K_3,3 polymer and another tetracyclic triply fused molecule with a ladder-type geometry. "I personally didn't believe they could be separated but he found the conditions to separate the two components completely," says Tezuka. "It's a very nice example of Japanese craftsmanship!"

The team are now in collaboration with simulation specialists with the aim of generalising the approach. "This paper is the basic proof of concept," says Tezuka. "There are many other structures that are not easy to make at the nanoscale."