Malaria: Blood cells behaving badly

All the billions of flat, biconcave disks in our body known as red blood cells (or erythrocytes) make three basic, tumbling-treadmill-type motions when they wend their way through the body's bloodstream ferrying oxygen from our lungs to our brains and other tissues. That is, unless they are infected with malaria parasites, in which case their motions are completely different.

A team of researchers at the National University of Singapore (NUS) has discovered this striking difference by comparing the flow dynamics of healthy vs. malaria-infected red blood cells. Reported this week in the Journal of Applied Physics, from AIP Publishing, their work may provide insights into developing better-targeted drug treatments for malaria in the future.

"By gaining a better understanding of why and how erythrocytes undergo changes in geometry and physical properties, we hope to elucidate such changes as possible targets for possible effective treatment of malaria," said Nhan Phan-Thien, a professor in the Department of Mechanical Engineering at the National University of Singapore.

Malaria, a life-threatening disease caused by Plasmodium parasites, afflicts hundreds of millions of people each year and is responsible for more than half a million deaths—mostly children living in Sub-Saharan Africa. Transmitted through the saliva of a female Anopheles mosquito, the parasites have a complicated, multi-stage life cycle part of which is spent inside the red blood cells of their human host.

Once the mosquito takes a blood meal and infects a person, malaria parasites invade red blood cells, making the cells stiffer and stickier. These cells also morph from a bi-concave shape to a more spherical form during the late "schizont stage" of malaria, which occurs 36 to 48 hours after onset of the infection. When red blood cells become stiff and deformed, they can become stuck in narrow capillaries and cause anemia, because fewer blood cells can flow to deliver oxygen to the different organs in the body, including the brain.

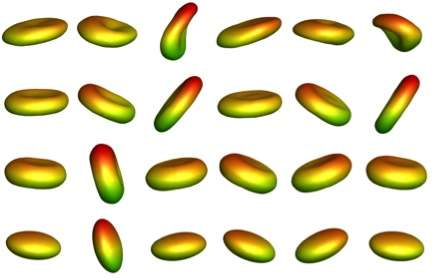
In the new paper, the NUS team reports how they used a particle-based method called "dissipative particle dynamics" to zero in on the three typical modes of motion of a cell or capsule in shear flow—tank-treading, tumbling, or trembling—and uncover the behavior of healthy and malaria-infected erythrocytes.

"Tank-treading mode is a steady state, in which a cell remains stationary while its membrane rotates around the internal fluid continuously," Phan-Thien explained. "Tumbling mode is an unsteady state in which the cell flips or tumbles periodically in its original shape as a rigid body. And the trembling mode is a transitional state between the two other modes, and is characterized by a shape variation and an angular oscillation."

The team discovered that, when experiencing the same shear rate, if a healthy erythrocyte undergoes a tumbling motion, the malaria-infected cell instead exhibits only a tumbling motion.

What advantage can malaria parasites gain by affecting the tumbling motion of erythrocytes? "Tumbling may allow the red blood cell to make better contact with the blood vessel wall and provide an opportunity to adhere to it," said Phan-Thien. The advantage to the parasite in making the red blood cell stick could be that it stalls the cells and keeps them from circulating and be cleared by the spleen or the immune system.

The researchers also found that at rates where a healthy erythrocyte undergoes a trembling motion, a malaria-infected cell can't exhibit the tank-treading motion. "And if a healthy erythrocyte undergoes a tank-treading motion, the malaria-infected one will exhibit any one of the three dynamic motions," noted Phan-Thien.