Advanced Analysis Tools Aim to Reduce Uncertainty in Climate Data
Pacific Northwest National Laboratory researchers have developed a new, advanced data-reduction method -- Stochastic Proper Orthogonal Decomposition -- that will greatly improve the capability to deal with uncertainty in the high-dimensional noisy data from random simulations.
Additionally, researchers have created a general approach for nonlinear bi-orthogonal decomposition of random fields to deal with uncertainty in climate model data as well as in measurements. Researchers have developed an efficient algorithm based on this approach to find the optimal positions for sensor placement to obtain climate data. This will help further reduce uncertainty in the data.
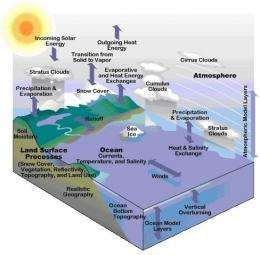
These results are part of a project funded by ASCR to analyze petascale, noisy data from global climate models and available experimental data to predict global warming scenarios.
If successful, the larger research project will have a revolutionary impact on how scientists analyze petascale, noisy, incomplete data in complex systems and ultimately lead to better future prediction and decision-making.
Extracting scientific knowledge from massive petascale data sets has become increasingly difficult and necessary as com puter systems have grown larger and experimental devices more sophisti cated. Petascale computers are capable of performing one quadrillion—one million billion—operations per second.
Numerical models and experimental approaches have their own limitations. Data-driven simulations at the petascale level could lead to great advances in accurately predicting the performance of dynamic data-driven systems. But the main bottleneck to reducing uncertainty is the ability to attract useful information from the petascale out puts of large-scale unsteady simulations. In addition, the uncertainty associ ated with the simulation inputs may render the results of these highly expensive simulations erroneous, especially in long-term predictions. Therefore, advanced data analysis tools, such as Stochastic Proper Orthogonal Decomposition, have to be developed to deal with petscale level noisy, incomplete data sets.
Noise-induced transition in the gradient systems, where the vector field is the gradient of a potential function, has been studied for a long time and understood very well. However, the understanding of transition events in non-gradient systems, such as climate system, is much less satisfactory. To effectively detect and predict the transition pathways in non-gradient systems, researchers have employed the minimum action method (MAM) derived from the large deviation theory. Researchers have successfully used the MAM method to detect the minimum action paths for the two dimensional noise-driven Ginzburgh-Laudau system and the Kuramoto-Sivashinsky equation.
Researchers will be applying the developed framework to climate science, where effective petascale data-reduction techniques are critical to analyzing the huge amount of numerical and experimental data generated from petaflop computers and high-throughput instruments.
More information: Wan, X, X Zhou and W E. 2010. "Study of the noise-induced transition and the exploration of the phase space for the Kuramoto-Sivashinsky equation using the minimum action methodaction method," Nonlinearity 23, 475-493.
Provided by Pacific Northwest National Laboratory