Physicist writes a better formula to predict baseball success
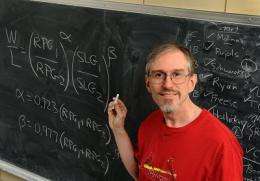
(PhysOrg.com) -- Kerry Whisnant, Iowa State University physicist, studies the mysteries of the neutrino, the elementary particle that usually passes right through ordinary matter such as baseballs and home-run sluggers.
Kerry Whisnant, St. Louis Cardinals fan, studies the mathematical mysteries of baseball, including a long look at how the distribution of a team's runs can affect the team's winning percentage.
Whisnant, a professor of physics and astronomy who scribbles the Cardinals' roster on a corner of his office chalkboard, is part of baseball's sabermetrics movement. He, like other followers of the Society for American Baseball Research, analyzes baseball statistics and tries to discover how all the numbers relate to success on the field.
The results are ideas, analyses, formulas and papers that dig deep into the objective data.
Whisnant recently took up a decades-old formula written by Bill James, the baseball author and statistician who inspired sabermetrics and is a senior adviser for baseball operations for the Boston Red Sox. The basic formula, which has been tweaked over the years, uses the number of runs scored per game (RPG) and runs given up per game to estimate a team's winning percentage.
Whisnant took that formula a step further by considering run distributions. What happens, in other words, when you consider how much a team's run production varies? Does it help if a team consistently scores runs? Does it hurt if a team scores a lot of runs one day and very few the next? And is slugging percentage (SLG, total bases divided by at bats) a good measure of that consistency?
Whisnant's answer, based on a Markov chain analysis that simplifies and simulates an infinite number of baseball games while eliminating the random fluctuations found by analyzing actual data from a finite number of games:
W1/L1 = (RPG1/RPG2)^a (SLG1/SLG2)^b
where
a = 0.723 (RPG1 + RPG2)^.373 and b = 0.977 (RPG1 + RPG2)^( -.947)
"I hated math in school, just write me a very condensed summary Kerry," a baseball fan wrote to dugoutcentral.com, a Web site for baseball talk and analysis, when Whisnant posted his formula there.
Whisnant's reply: "Bottom line: More consistent teams (narrower run distribution) tend to win more games for the same RPG (runs per game). Teams with higher SLG (slugging percentage) tend to have a narrower run distribution. Given two teams with the same RPG, a team with a SLG .080 higher will on average win one more game a season. If their pitching/defense has the same RPG allowed but a SLG allowed .080 lower, that would add another game."
So there you have it: "The more consistent a team is in scoring runs, game to game, the better the team's winning percentage for the total number of runs scored," Whisnant said.
"My study shows that runs alone don't tell the whole story," he said. "Consistency is another factor. You want to score runs, and you want to be consistent."
Across an entire 162-game season, Whisnant said more consistency could mean two additional wins. And that can be the difference between making the playoffs and calling it quits the first week in October.
Whisnant's paper explaining the formula was recently named one of four finalists in a contest sponsored by the Massachusetts Institute of Technology's Sloan Sports Analytics Conference in Boston on March 6.
And while he's at the conference to present his paper, other baseball researchers are telling Whisnant to introduce himself to general managers of Major League Baseball teams. You never know, maybe the Cardinals are looking for a statistical consultant.
Nothing against neutrinos, Whisnant said, "but it would be a dream job to be a part-time analyst for the Cardinals."
Provided by Iowa State University
















