Surprising mathematical law tested on Project Gutenberg texts
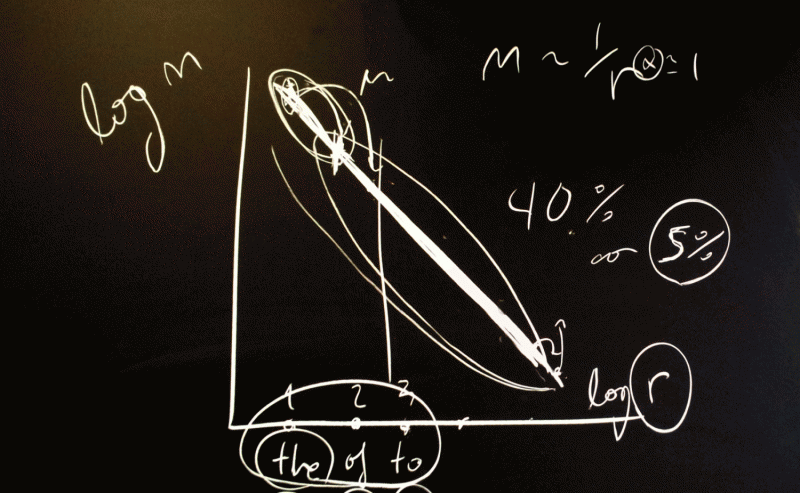
Zipf's law in its simplest form, as formulated in the thirties by American linguist George Kingsley Zipf, states surprisingly that the most frequently occurring word in a text appears twice as often as the next most frequent word, three times more than the third most frequent one, four times more than the fourth most frequent one, and so on.
The law can be applied to many other fields, not only literature, and it has been tested more or less rigorously on large quantities of data, but until now had not been tested with maximum mathematical rigour and on a database large enough to ensure statistical validity.
Researchers at the Centre de Recerca Matemàtica (CRM), part of the Government of Catalonia's CERCA network, who are attached to the UAB Department of Mathematics, have conducted the first sufficiently rigorous study, in mathematical and statistical terms, to test the validity of Zipf's law. This study falls within the framework of the Research in Collaborative Mathematics project run by Obra Social "la Caixa". To achieve this, they analysed the whole collection of English-language texts in the Project Gutenberg, a freely accessible database with over 30,000 works in this language. There is no precedent for this: in the field of linguistics the law had never been put to the test on sets of more than a dozen texts.
According to the analysis, if the rarest words are left out - those that appear only once or twice throughout a book - 55% of the texts fit perfectly into Zipf's law, in its most general formulation. If all the words are taken into account, even the rarest ones, the figure is 40%.
"It is very surprising that the frequency of occurrence of these words should be determined by a single-parameter formula. The famous Gaussian bell curve, for example, needs two parameters, position and width, to adjust to the real data", explains Álvaro Corral, a CRM researcher attached to the UAB Department of Mathematics and coordinator of the research. "If we ignored words that appear three, four or five times in a whole work, the percentage of books that follow Zipf's law could be even higher".
In mathematical terms, the law states that if all the words are ranked by frequency of use, the second most frequently occurring one appears half as often as the most frequent one; the third, 1/3 as often and, in general, the word occupying the position n appears 1/n times as often as the most frequent one.
In fact, the most general formulation of the law includes an exponent a, so that the relationship is 1/na. Though this complicates the formula a little, the frequency fits very closely for values of "a" very near to 1 (i.e. as if no exponent had been added). There are other formulations of the law that are mathematically more complex, but all have a single free parameter.
The researchers studied the validity of the three most frequently used formulations of Zipf's law in all the English-language texts (31,075 books) in the Project Gutenberg database, and they observed that one of these formulations fits, with statistically significant results (p>0.05), the frequency of occurrence of all the words in over 40% of the books in the collection, texts that contain between 100 and over a million words.
"Zipf's law has generated much debate, but always basing its validity on certain specific examples", points out Álvaro Corral. "It seems obvious that in today's age of Big Data and high-performance computers, we need to focus on large-scale analysis of the law, and these results are a big step in that direction".
"Although literature is regarded as one of the greatest expressions of creative freedom, not even major authors like Shakespeare or Dickens escape the tyranny of Zipf's law", concludes Dr Corral.
More information: Isabel Moreno-Sánchez et al. Large-Scale Analysis of Zipf's Law in English Texts, PLOS ONE (2016). DOI: 10.1371/journal.pone.0147073
Journal information: PLoS ONE
Provided by Universitat Autonoma de Barcelona