Improving electric motor efficiency via shape optimization

In our competitive global society, successful and economical design of automotive and industrial structures is crucial. Optimizing the geometry of individual pieces of complex machines improves performance and efficiency of the entire device.
To achieve this, the automotive and aeronautic industries often rely on shape optimization, an approach that uses modeling to create a framework for making devices as smooth and efficient as possible. "A smoother rotation of the rotor can increase the energy efficiency of the motor, and at the same time reduce unwanted side effects like noise and vibrations," says mathematician Ulrich Langer.
Langer, along with Peter Gangl, Antoine Laurain, Houcine Meftahi, and Kevin Sturm, co-authored a paper publishing tomorrow in the SIAM Journal on Scientific Computing that utilizes shape optimization techniques to enhance the performance of an electric motor. "By means of shape optimization methods, optimal motor geometries which could not be imagined beforehand can now be determined," says Langer.
Shape optimization problems are typically solved by minimizing the cost function, a mathematical formula that predicts the losses (or 'cost') corresponding with a process; the end goal is the creation of an optimal shape, one that minimizes the cost function while meeting certain constraints.
Langer and his coauthors apply optimization techniques to an interior permanent magnet (IPM) brushless electric motor, the kind sometimes used in washing machines, computer cooling fans, and assembly tools. The motor's inner rotor contains an iron core and permanent magnets. Because not all parts of the rotor's geometry are able to be altered, the authors identify a modifiable design subregion in the rotor's iron core on which to apply shape optimization. Their objective is to improve the workings of the rotor, thus resulting in a smoother, more desirable rotation pattern.
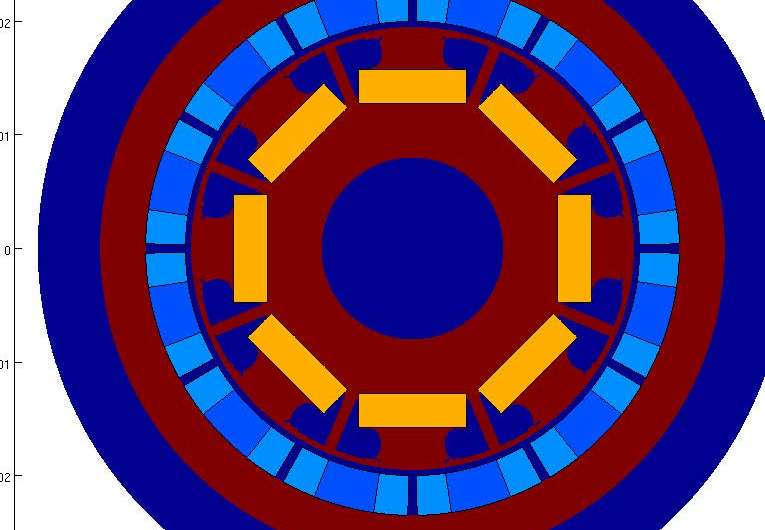
"Differentiating with respect to the shape is more complicated than differentiating a function," says Antoine Laurain. "In fact, there are many ways to define shape perturbations and differentiation with respect to shapes. The so-called 'shape derivative' is one incarnation of these possibilities. It allows us to explore a wide range of possible geometries for the optimization." Unlike the topological derivative, which generates a shape with uneven contours, the shape derivative employs a smooth alteration of the boundary. Implementing the obtained shape derivative in a numerical algorithm provides a shape that allows the authors to improve the rotation pattern.
The authors' optimization procedures stem from Lagrangian methods for approaching nonlinear problems, and demonstrate an efficient, exact means of calculating the shape derivative of the cost function. This simple and comprehensive method allows for the treatment of nonlinear partial differential equations (PDEs) and general cost functions, rather than only linear PDEs. Ultimately, their optimization procedures are able to achieve a 27 percent decrease in the cost functional of an IPM brushless electric motor, the particular example explored in the paper.
Now that they have effectively utilized a shape derivative in optimization, the authors hope to experiment further in the future. "We are currently working on the derivation of the so-called 'topological derivative' for the same nonlinear optimization problem," says Peter Gangl. "This quantity indicates regions where a local change of the material would lead to a decrease of the objective function."
For now, their application of mathematics in the form of a shape-Lagrangian method adapted for nonlinear PDEs results in a shape that improves the electric rotor's rotation pattern and the motor's overall performance.
More information: Shape Optimization of an Electric Motor subject to Nonlinear Magnetostatics, SIAM Journal on Scientific Computing (to be published online on December 22, 2015).
Provided by Society for Industrial and Applied Mathematics