June 9, 2014 feature
Four-color theorem linked to crystal's magnetic properties
(Phys.org) —Sometimes mathematical theories have implications that extend far beyond their original purpose. This situation holds true for the four-color theorem, which was originally used by cartographers hundreds of years ago to draw maps. According to the theorem, four colors are sufficient to color different countries on a 2D map so that no two adjacent countries have the same color (excluding intersecting corners). However, today the four-color theorem is less interesting to cartographers than it is to mathematicians due to the complexity of its proof, which was achieved in 1976.
Now, a team of mathematicians, physicists, and chemists from the US, South Korea, and Japan has discovered that the four-color theorem can be used to understand the crystal structure and magnetic properties of a complex material. Their paper is published in a recent issue of the Journal of the American Chemical Society.
"Most technological materials such as steels or magnets exhibit complex domain structures, which often determine macroscopic physical properties," Sang-Wook Cheong, Professor at both Rutgers University in Piscataway, New Jersey, and at the Pohang University of Science and Technology in Pohang, South Korea, told Phys.org. "Our paper, for the first time, demonstrated that the configuration of domain structures can be understood in terms of mathematics, specifically color theorems.
The material that the researchers analyzed is iron-intercalated tantalum disulfide (FexTaS2), which belongs to a class of materials called layered transition metal dichalcogenides (TMDs). In this material, when thin layers of the TMD TaS2 are intercalated with Fe ions, the resulting "superstructure" gives rise to new crystal structures that modify the material's physical properties.
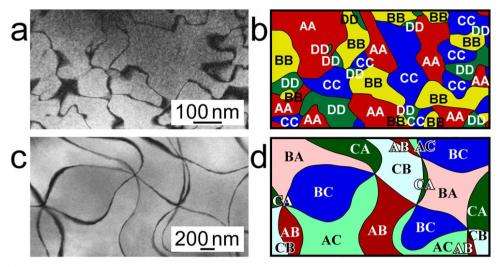
The researchers investigated FexTaS2 where the intercalated Fe ions order and form two different superstructures with different in-plane Fe-Fe distances for x=1/4 and x=1/3. Using a transition electron microscope (TEM), the researchers could observe that these different superstructures produce very different crystal domain patterns. For example, the superstructures have different stacking sequences, different domain sizes, and different numbers of domain types (four when x=1/4 and six when x=1/3).
If the different domain types are thought of as countries on a map, they can be colored in accordance to different versions of the color theorem. The Fe1/4TaS2 superstructure makes for a straightforward pattern in which the four domain types can be colored with four colors, corresponding to the traditional four-color theorem. Mathematically speaking, it is 4-colorable.
However, Fe1/3TaS2 is more complicated. It has the unusual characteristic that six domain boundaries always merge at one point without exception. This pattern is called a "6-valent graph." Furthermore, each domain is always surrounded by an even number of vertices, forming a so-called "even-gon."
As a result of these unique characteristics, Fe1/3TaS2 corresponds to a two-step version of the color theorem. Whereas the Fe1/4TaS2 superstructure is 4-colorable, the Fe1/3TaS2 superstructure is 2 x 3-colorable. That means that the first step involves coloring domains as either dark or light, after which the dark and light domains are colored with one of three colors (such as red, blue, and green). The resulting domain map is colored in such a way that each domain is not adjacent to another domain with the same "first" color nor the same "second" color. For example, a dark red domain is never adjacent to a light red domain or any dark domain.
Of course, there is nothing inherent about crystal domains being colored in a certain way. Instead, the color theorems provide an intuitive way to understand a material's complex domain topology. In turn, the domain topology is closely related to each material's magnetic properties. Specifically, the 4-colorable domains are associated with a strong pinning effect of magnetic domain walls, while the 2 x 3-colorable domains accompany a weak pinning of magnetic domain walls.
In the future, understanding domain wall patterns may enable researchers to control and exploit these macroscopic physical properties of materials by modifying the materials' topologies. This ability could lead to a wide range of applications in electronic, magnetic, and optical devices.
"We will attempt to generalize multi-step color theorems and to explore new domain structures that can be understood with generalized color theorems," Cheong said. "Ultimately our understanding of domains with color theorems will help us to manipulate domain structures to optimize functionalities of materials."
More information: Yoichi Horibe, et al. "Color Theorems, Chiral Domain Topology, and Magnetic Properties of FexTaS2." Journal of the American Chemical Society. DOI: 10.1021/ja5026134
Journal information: Journal of the American Chemical Society
© 2014 Phys.org