November 12, 2013 report
Statistician suggests raising statistical standards to reduce amount of non-reproducible studies
(Phys.org) —Valen Johnson, a statistician with Texas A&M University is suggesting in a paper published in Proceedings of the National Academy of Sciences, that the statistical standard used to judge the soundness of research efforts be made more stringent. Doing so, he writes, would reduce the large numbers of non-reproducible findings by researchers and as a result prevent the undermining of confidence in such efforts.
Over the past few years, the number of research papers being published that claim to have made certain findings, but which can't be reproduced by others in the field has increased, leading to calls for changes to be made in how such efforts are graded.
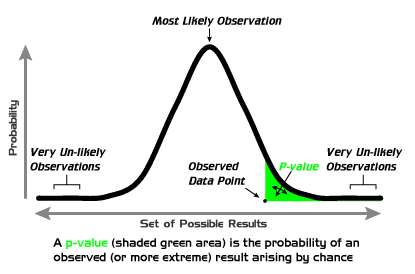
The traditional approach is based on a P value—a number obtained by comparing an alternative hypothesize against a null value (what it would be if left alone). This number is supposed to give the researcher an idea of whether his or her efforts have resulted in a change to whatever it is they are investigating. Convention argues that a P value of 0.05 is statistically significant enough to claim that something has indeed been changed, which means the researchers can claim success in their endeavor. But, Johnson argues, there is a serious flaw in this approach. He argues that the P value actually represents the likelihood of an extreme value occurring in an experiment, and thus doesn't truly reflect the degree of variation from the norm that researchers believe it to be.
In statistics, there is a another way to calculate the difference between the norm and results obtained by causing a change to a system, it's called Bayesian Hypothesis testing and it, Johnson explains, offers a way to calculate a genuine comparison. To strengthen his point, he has devised a way to convert a Bayes factor to P values. Doing so, he argues shows just how weak P values can be.
The problem, he writes, is not that researchers use P values, but that they rely on values for it that are not stringent enough. He suggests the research community change its standard of acceptance from .05 to .005 or even to .001. That he believes, would greatly reduce the number of research papers with un-reproducible results being published, saving reputations and reduce money spent on wasted follow-up research efforts.
More information: Revised standards for statistical evidence, PNAS, Published online before print November 11, 2013, DOI: 10.1073/pnas.1313476110
Abstract
Recent advances in Bayesian hypothesis testing have led to the development of uniformly most powerful Bayesian tests, which represent an objective, default class of Bayesian hypothesis tests that have the same rejection regions as classical significance tests. Based on the correspondence between these two classes of tests, it is possible to equate the size of classical hypothesis tests with evidence thresholds in Bayesian tests, and to equate P values with Bayes factors. An examination of these connections suggest that recent concerns over the lack of reproducibility of scientific studies can be attributed largely to the conduct of significance tests at unjustifiably high levels of significance. To correct this problem, evidence thresholds required for the declaration of a significant finding should be increased to 25–50:1, and to 100–200:1 for the declaration of a highly significant finding. In terms of classical hypothesis tests, these evidence standards mandate the conduct of tests at the 0.005 or 0.001 level of significance.
* Read also this The Conversation article.
Journal information: Proceedings of the National Academy of Sciences
© 2013 Phys.org