Liquid crystal research, future applications advance

Contributing geometric and topological analyses of micro-materials, University of Massachusetts Amherst mathematician Robert Kusner aided experimental physicists at the University of Colorado (UC) by successfully explaining the observed "beautiful and complex patterns revealed" in three-dimensional liquid crystal experiments. The work is expected to lead to creation of new materials that can be actively controlled.
Kusner is a geometer, an expert in the analysis of variational problems in low-dimensional geometry and topology, which concerns properties preserved under continuous deformation such as stretching and bending. His work over 3 decades has focused on the geometry and topology of curves, surfaces and other spaces that arise in nature, such as soap films, knots and the shapes of fluid droplets. Kusner agrees with physicist and lead author Ivan Smalyukh of UC Boulder that their collaboration is the first to show in experiments that some of the most fundamental topological theorems hold up in real materials. Their findings appear in the current early online issue of Nature.
UMass Amherst's Kusner explains, "There are two important aspects of this work. First, the experimental work by the Colorado team, who fabricated topologically complex micro-materials allowing controlled experiments of three-dimensional liquid crystals. Second, the theoretical work performed by us mathematicians and theoretical physicists while visiting the University of California Santa Barbara's Kavli Institute for Theoretical Physics (KITP). We provided the geometric and topological analysis of these experiments, to explain the observed patterns and predict what patterns should be seen when experimental conditions are changed."
Kusner was the lone mathematician among four organizers of last summer's workshop on "Knotted Fields" at KITP, which led to this work. The workshop engaged about a dozen other mathematicians and about twice as many theoretical and experimental physicists in a month-long investigation of the interplay between low-dimensional topology and what physicists call "soft matter."
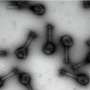
In their experiments, the physicists at UC Boulder showed that tiny topological particles injected into a liquid crystal medium behave in a manner consistent with established theorems in geometry and topology, Kusner says. The researchers say they have thus identified approaches for building new materials using topology.
UC Boulder's Smalyukh and colleagues set up the experiment by first creating colloids, solutions in which tiny particles are dispersed but not dissolved in a host medium, such as milk, paint and shaving cream. Specifically, they injected tiny, different-shaped particles into a liquid crystal, which behaves something like a liquid and a solid. Once injected into a liquid crystal, the particles behaved as predicted by topology.
Smalyukh says, "Our study shows that interaction between particles and molecular alignment in liquid crystals follows the predictions of topological theorems, making it possible to use these theorems in designing new composite materials with unique properties that cannot be encountered in nature or synthesized by chemists. These findings lay the groundwork for new applications in experimental studies of low-dimensional topology, with important potential ramifications for many branches of science and technology."
For example, he adds, these topological liquid crystal colloids could be used to upgrade current liquid crystal displays like those used in laptops and television screens, to allow them to interact with light in new, more energy efficient ways.
Journal information: Nature
Provided by University of Massachusetts Amherst