Riding a bike couldn't be ... more complicated
We are told there's nothing easier than riding a bike. The reality is when it comes to staying upright, there is nothing more complicated. The mathematical formula which explains the motion of a bicycle looks like it could be used to split the atom and took scientists from three different countries years to devise.
It also explains the frustration and angst suffered by so many dads watching their struggling youngsters totter, wobble and crash as they attempt to master two wheels for the first time.
The complex equation, which uses 31 numbers and symbols, plus nine pairs of brackets, looks like this:
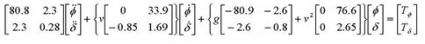
What this actually boils down to is:
Inertia forces + gyroscopic forces + the effects of gravity and centrifugal forces = the leaning of the body and the torque applied to the handlebars of a bike.
Or put more simply if you don’t peddle fast enough to keep moving while keeping the bike straight, you fall over.
The equation produced by boffins from universities in Holland, the USA and Nottingham has come to light during research by Halfords to compile tips for parents teaching their children to ride a bike.
With National Cycle Week starting Mon June 20, more people than ever are being encourage to get on a bike and Halfords was hoping to help cut down on the agony suffered by youngsters when going though that rite of passage when first taking to two wheels.
Commercial Director, Paul McClenaghan said “It turns out that getting off on the right foot on a bicycle, ditching the stabilisers and speeding away from your anxious parents is actually much more complex that people realised.
“Once you master the technique as the saying goes it’s something you never forgot, but there is a great deal of science behind the skill. We make all our own bikes and are hoping that this work will help make bike riding as easy as possible.”
Dr Arend Schwab of Delft University of Technology in the Netherlands who helped develop the equation explains that ever since the inventions of the bicycle in the 1860’s mathematicians have been trying to use Newton’s laws of motion to explain its unique movement and ability to balance.
“People more than a hundred years ago were trying to figure out why a two wheeled bicycle, given forward momentum, like a push, would seem to balance by itself,” said Dr Schwab.
The meticulous mathematical account of bike riding and their continued research may eventually lead to better bike design with improved stability and safety, something that has also attracted the attention of British bike retailing giant Halfords.
Dr Schwab explained: “Using our equation we can simulate the motion of a bike and predict whether it will remain stable or not, under certain conditions, such as if it goes over a bump, or is hit by a gust of wind.
“This equation is aimed at enabling a bike designer to change certain features and to see the overall finished effect on the bike, without having to actually manufacture it first.
“For instance if you are designing a folding bike with smaller wheels or one with a shorter wheel base this equation allows you to interpret how design changes will affect the stability and behaviour of the bike,” Dar Schwab added.
More information:
-- For further information on Dr Schwab and his colleagues’ research, visit: audiophile.tam.cornell.edu/~al … 93/Bicycle/index.htm
-- Research paper: J. P. Meijaard, Jim M. Papadopoulos, Andy Ruina, A. L. Schwab, 2007 ``Linearized dynamics equations for the balance and steer of a bicycle: a benchmark and review,'' Proceedings of the Royal Society A 463:1955-1982. doi:10.1098/rspa.2007.1857
Provided by Halfords