Quantum age edges closer
(PhysOrg.com) -- The arrival of superfast quantum computing is closer following recent breakthroughs by an international team led by UNSW researchers.
Superfast quantum computing is closer than ever following recent breakthroughs by an international team led by researchers from the University of New South Wales.
Quantum computing relies on controlling and observing the behaviour of quantum particles - for instance individual electrons - to deliver enormous processing power.
In the two breakthroughs, written up in the international journals Nano Letters and Applied Physics Letters, researchers have for the first time demonstrated two ways to deliberately place an electron in a nano-sized device on a silicon chip.
The achievements set the stage for the next crucial steps of being able to observe and then control the electron’s quantum state or "spin", to create
a quantum bit.
Multiple quantum bits coupled together make up the processor of a quantum computer.
Professor Andrew Dzurak, the NSW Node Director of the Australian National Fabrication Facility at UNSW and Dr Andrea Morello, Manager of the Quantum Measurement and Control Chip Program at the ARC Centre of Excellence for Quantum Computer Technology, were leaders in the breakthrough work.
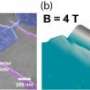
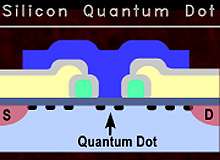
In research just published in Applied Physics Letters, the team, including PhD student Wee Han Lim, were able to accurately localise a single electron in silicon without it being attached to an atom. This “artificial atom” is known as a “quantum dot”.
Dr Morello said the quantum dot avoided the difficulty of having to introduce single atoms in precise positions in a silicon chip.
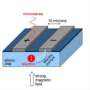
In a separate project, published in the journal Nano Letters, the researchers, including PhD student Kuan Yen Tan, used "nature’s own way" to localise electrons, by binding them to single atoms.
Quantum computing’s power comes from the fact that electrons can have a "spin" pointing in one of two directions. The spin position can be used in the same way that zeroes and ones represent data in today’s computers.
However electrons can also hold intermediate spin positions, or quantum states, which is what gives quantum computing its power.
While today's computers increase their power linearly with the number of bits added, quantum bits, when coupled together, can deliver an exponential increase in their ability to represent data.
The other leaders of the research team are Professor David Jamieson at the University of Melbourne, and Dr Mikko Möttönen at the Helsinki University of Technology. Students Wee Han Lim and Kuan Yen Tan have just completed their PhD degrees in the UNSW School of Electrical Engineering and Telecommunications.
More information: -- Applied Physics Letters paper: scitation.aip.org/getabs/servl … dtype=cvips&gifs=yes
-- Nano Letters paper: pubs.acs.org/doi/abs/10.1021/n … ak&searchHistoryKey=
Provided by University of New South Wales