Everlasting Quantum Wave: Physicists Predict New Form of Soliton in Ultracold Gases
(PhysOrg.com) -- Solitary waves that run a long distance without losing their shape or dying out are a special class of waves called solitons. These everlasting waves are exotic enough, but theoreticians at the Joint Quantum Institute (JQI) , a collaboration of the National Institute of Standards and Technology and the University of Maryland, and their colleagues in India and the George Mason University, now believe that there may be a new kind of soliton that’s even more special. Expected to be found in certain types of ultracold gases, the new soliton would not be just a low-temperature atomic curiosity, it also may provide profound insights into other physical systems, including the early universe.
Solitons can occur everywhere. In the 1830s, Scottish scientist John Scott Russell first identified them while riding along a narrow canal, where he saw a water wave maintaining its shape over long distances, instead of dying away.
his “singular and beautiful” phenomenon, as Russell termed it, has since been observed, created and exploited in many systems, including light waves in optical-fiber telecommunications, the vibrational waves that sweep through atomic crystals, and even “atom waves” in Bose-Einstein condensates (BECs), an ultracold state of matter. Atoms in BECs can join together to form single large waves that travel through the gas. The atom waves in BECs can even split up, interfere with one another, and cancel each other out.
In BECs with weakly interacting atoms, this has resulted in observations of “dark solitons,” long-lasting waves that represent absences of atoms propagating through the gas, and “bright” solitons (those carrying actual matter).
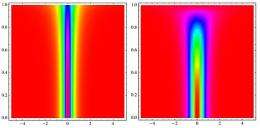
By taking a new theoretical approach, the JQI work predicts a third, even more exotic “immortal” soliton—never before seen in any other physical system. This new soliton can occur in BECs made of “hard-core bosons”—atoms that repel each other strongly and thus interact intensely —organized in an egg-crate-like arrangement known as an “optical lattice.” In 1990, one of the coauthors of the present work, Radha Balakrishnan of the Institute of Mathematical Sciences in India, wrote down the mathematical description of these new solitons, but considered her work merely to approximate the behavior of a BEC made of strongly interacting gas atoms.
With the subsequent observations of BECs, the JQI researchers recently realized both that Balakrishnan’s equations provide an almost exact description of a BEC with strongly interacting atoms, and that this previously unknown type of soliton actually can exist. While all previously known solitons die down as their wave velocity approaches the speed of sound, this new soliton would survive, maintaining its wave height (amplitude) even at sonic speeds.
If the “immortal” soliton could be created to order, it could provide a new avenue for investigating the behavior of strongly interacting quantum systems, whose members include high-temperature superconductors and magnets. As atoms cooling into a BEC represent a phase transition (like water turning to ice), the new soliton could also serve as an important tool for better understanding phase transitions, even those that took place in the early universe as it expanded and cooled.
More information: R. Balakrishnan, I.I. Satija and C.W. Clark, “Particle-hole asymmetry and brightening of solitons in a strongly repulsive Bose-Einstein condensate,” Physical Review Letters, vol. 103, p. 230403; published online Dec. 4, 2009.