Determining refractive index at relativistic speeds

If you studied advanced physics at high school, there's a good chance that you remember Snell's law, which states how a ray of light bends when it crosses a boundary between two media. According to this law, the ratio of the sines of the incident and refracted angles is a non-universal constant, later understood as the relative refractive index of the refracting medium with respect to the incident one.

The theoretical formulation of the law of optical refraction was initiated by Descartes in the early 17th century. He introduced a metaphysical form of an optical-mechanical analogy, suggesting a conceptual parallel between trajectories in classical mechanics and wavefronts in optics.

Descartes considered the conservation of the tangential component of the velocity of a particle, as well as light, as it crosses a boundary between media. He determined the relative refractive index as the ratio of the speed of light in the two media. Later this century, Descartes' metaphysical theory was rejected by Fermat by introducing the "least time principle" that was named after him. He also determined the relative refractive index as the ratio of the speed of light in the two media.

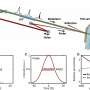
Descartes' idea, which pre-dates the discovery that the speed of light is finite was "brilliant." It needed a relativistic theory that was formulated much later in the early 20th century. Shyamal Biswas and his research group members at the University of Hyderabad in India have now extended Descartes' metaphysical theory to determine the mechanical refractive index for relativistic particles entering media at all possible speeds. This work has now been published in the journal The European Physical Journal D.

Biswas and his co-workers defined the mechanical refractive index by comparing the Helmholz wave equation for light in an optical medium and the time-independent Klein-Gordon equation for a relativistic particle in a potential. "Our analytical method involved only quite simple mathematics: algebra, trigonometry, and calculus," he explains.

The researchers' calculations of the mechanical refractive index for particles traveling at different speeds up to that of light exactly matches with Descartes' result at the non-relativistic limit and Fermat's result at the ultra-relativistic limit. "Our calculations may have applications in studying the transmission and reflection of particles in mechanical media," concludes Biswas.