A universal framework describing the scrambling of quantum information in open systems

In recent years, physicists have been trying to better understand how quantum information spreads in systems of interacting particles—a phenomenon often referred to as "scrambling." Scrambling in closed systems, physical systems that can only exchange energy with degrees of freedom within the system, is a characteristic feature of chaotic many-body quantum dynamics.

In open systems, which can exchange both energy and matter with their surroundings, scrambling is influenced by various additional factors, including noise and errors. While the effects of these additional influences are well-documented, leading for example to decoherence, how they affect scrambling remains poorly understood.

Two researchers from the University of California Berkeley (UC Berkeley) and Harvard University recently introduced a new framework, published in Physical Review Letters, that provides a universal picture for how information scrambling occurs in open quantum systems. Their framework offers a particularly simple viewpoint on how to understand and model the propagation of errors in an open quantum system and might already help to explain some previously puzzling observations gathered in magnetic resonance experiments.

"Norm and I have worked on several projects together focusing on quantum information scrambling before," Thomas Schuster, one of the researchers who carried out the study, told Phys.org.

"Some of our works focused on how to measure scrambling, and others on what scrambling might be useful for. In all of these projects, a natural question kept coming up: How is scrambling modified by errors (that is, 'open-system' dynamics) that inevitably occur in real-life experiments? Although this question was clearly important, we did not have any satisfying framework for answering it."

While exploring this question, Schuster and Yao realized that it might be helpful to consider things from an experimental perspective. This ultimately led to their recent study.

"In open-system dynamics, errors perturb the system, and we would like to know the sensitivity of our experiment to these perturbations," Schuster said. "This suggests that the sensitivity of an experiment to errors must be related to how information scrambles. Building on this initial idea, we worked to make the connection between errors and scrambling precise, and to analyze its consequences for physical systems and experiments of interest."

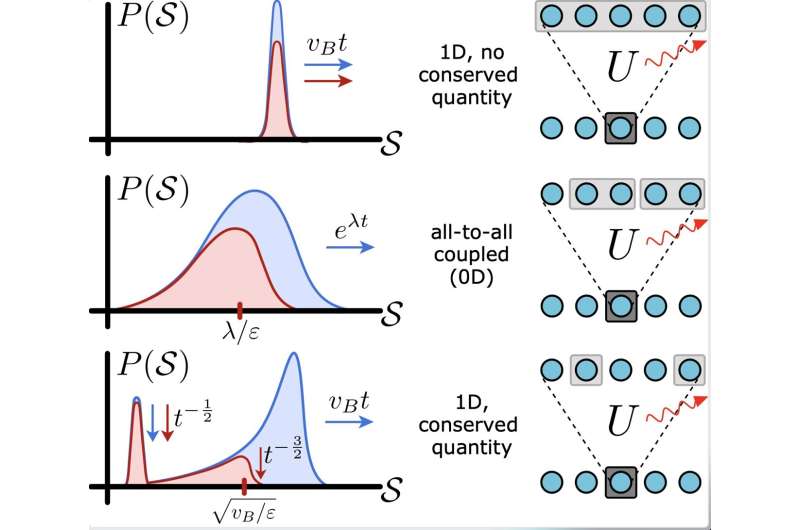
The key idea behind the recent study by Schuster and Yao is that information scrambling in an open system is somewhat independent of the microscopic nature of the errors themselves. Rather, it all depends on how these errors affect the so-called "operator size distributions," a characterization of the operator's complexity under time evolution.

"The dynamics of the operator size distribution determine how errors spread in a precise way," Schuster explained. "At its simplest level, this takes the form of two coupled differential equations. The input to the equations is how the distribution of operator sizes changes while the output can be thought of as a sharp prediction for how errors spread."

While some previous studies had hinted at this connection, no one had clearly and precisely formulated it so far. In doing so, Schuster and Yao found that the interplay between errors and scrambling was much more nuanced than had been previously anticipated.

"Another novel result from our work is that errors also modify the behavior of information scrambling itself," Schuster said. "This leads to an interesting interplay between errors and scrambling, described by the equations mentioned above. The outcome of this interplay depends on the nature of the dynamics themselves and can be used as an intrinsic characterization of these dynamics, in addition to predicting various properties of experiments."

A particularly fruitful setting for applying the framework of Schuster and Yao arises in certain experiments that involve so-called "ergodic" many-body dynamics. This could be carried out and validated in future works.

"A pleasant surprise that we discovered as we were completing our results is that our framework also applies to a large class of experiments—called the 'Loschmidt echo'—which have been of interest to the nuclear magnetic resonance (NMR) and quantum chaos communities for several decades," Schuster said. "The Loschmidt echo is a long-standing thought experiment in thermodynamics, dating back to Josef Loschmidt and the foundation of thermodynamics in the 1800s."

While experimental methods surrounding the Loschmidt echo have continued to improve, both in quantum simulation experiments as well as solid-state magnetic resonance studies, interpreting these signals, especially for interacting Hamiltonians in the latter context, has continued to be challenging.

"Experimentalists would fit various functional forms (for example, Gaussians or exponentials or sigmoids) to their data, but never had an explanation for why a specific experiment followed one functional form instead of another," Schuster said. "In the early 2000s, researchers discovered a framework for how to describe the Loschmidt echo in few-body quantum systems; however, the case of many-body systems has remained an open question. We believe that our framework may provide an answer to this question."

In addition to shedding light on how errors propagate in open many-body quantum systems, the recent work also suggests that data from Loschmidt echo experiments could contain more information than originally meets the eye.

"The interplay of errors and operator size distribution dynamics determines the functional form of the Loschmidt echo," Schuster said. "We are confident that this is the case in the toy models that we can numerically study, and in future work, we hope to provide a more detailed analysis of Loschmidt echo experimental data to confirm that our framework applies there as well. There are several indications that strongly suggest it does, which I find to be quite exciting."

Looking forward, Schuster and Yao are interested in applying their new framework to a variety of other experiments. They also plan to explore the implications of their results for the classical simulation of open quantum systems.

"We're wondering whether our understanding of information spreading in these open systems can actually provide insight into how much quantum advantage can be harnessed from them," says Yao. "And on the flip-side, whether one can then design new algorithms to efficiently simulate open quantum systems."

© 2023 Science X Network