'Swarmalators' better envision synchronized microbots

Imagine a world with precision medicine, where a swarm of microrobots delivers a payload of medicine directly to ailing cells. Or one where aerial or marine drones can collectively survey an area while exchanging minimal information about their location.

One early step towards realizing such technologies is being able to simultaneously simulate swarming behaviors and synchronized timing—behaviors found in slime molds, sperm and fireflies, for example.

In 2014, Cornell researchers first introduced a simple model of swarmalators—short for "swarming oscillator"—where particles self-organize to synchronize in both time and space. In the study, "Diverse Behaviors in Non-uniform Chiral and Non-chiral Swarmalators," which published Feb. 20 in the journal Nature Communications, they expanded this model to make it more useful for engineering microrobots; to better understand existing, observed biological behaviors; and for theoreticians to experiment in this field.

"We wanted a simple mathematical model that can lay the foundation for swarmalators in general, something that captures all of the complex emergent phenomena we see in natural and engineered swarms," said Kirstin Petersen, the paper's senior author, assistant professor and an Aref and Manon Lahham Faculty Fellow in the Department of Electrical and Computer Engineering in Cornell Engineering.

Steven Ceron, Ph.D., a former graduate student in Petersen's lab, is the paper's first author, and Kevin O'Keeffe Ph.D., a former graduate student in applied mathematics, is a co-author.

O'Keeffe compared this model to the largest doll in a set of Russian dolls, with each smaller doll representing models capable of simulating more refined behaviors. "We've tried to come up with a model that is as simple as possible in the hope of capturing generic phenomena," he said.

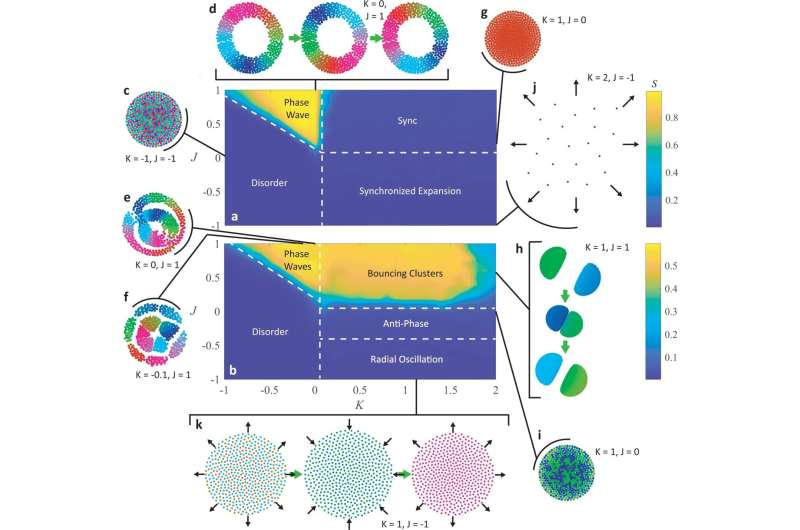
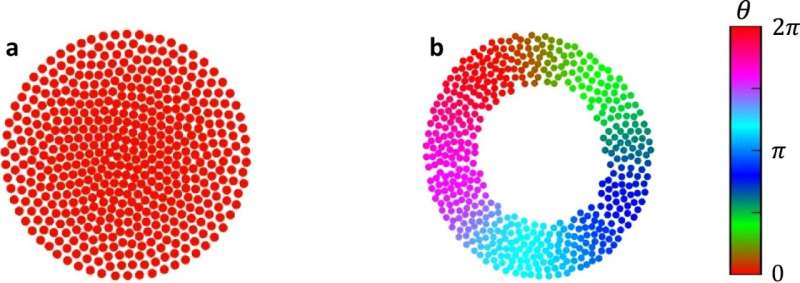
The researchers simplified their model to work with just four mathematical constants linked together to produce diverse emergent behaviors, such as aggregation, dispersion, vortices, traveling waves, and bouncing clusters.

The new model can mimic particles in nature that each operate at different natural frequencies, as some objects move slower and faster around a trajectory than others. The researchers also added chirality, or the ability for a particle to move in a circle, because many examples in nature, such as sperm, swim in circles and in vortices. And particles in the model exhibit local coupling, so they sense and respond only to their local neighbors.

At its core, the model combines swarming behaviors with synchronization in time. Examples of swarming from nature include flocking birds or herds of stampeding buffalo, where individuals move together as a group. Synchronized timing can be found in cardiac pacemaker cells that fire an electric impulse in unison, shocking the heart into regular repeated beats. Sperm represent both phenomena together, as they can beat their tails in unison while swimming as a group. Fireflies are also known to fly in swarms while flashing in synchrony.

"That's what makes them swarmalators, because there's two of the self-organizing forces going on at the same time," O'Keeffe said.

The model doesn't try to model a specific real world swarmalator, such as sperm, robotic drones, or magnetic domain walls. Rather, it tries to model the behavior common to all those systems—it aims for generality, rather than specificity. As an example, the model was shown to reproduce behaviors found in microbial slime molds, which can operate as individual cells, but when starved will aggregate into a slug and eventually a fruiting body.

"These very simple coupled mechanisms can potentially be implemented on swarms of tiny robots with very limited power, computational and memory resources, which in spite of their individual simplicity can work together to produce the complex swarming behaviors we predict in our model," Petersen said.

One future application could be for precision medicine, where tiny magnetized insoluble particles could swarm and be synchronized in relation to each other and then controlled to deliver a payload to tissues in need of a therapy, O'Keeffe said.