March 14, 2023 feature

Editors' notes

This article has been reviewed according to Science X's editorial process and policies. Editors have highlighted the following attributes while ensuring the content's credibility:

fact-checked

peer-reviewed publication

trusted source

proofread

Quantum chemistry simulations on a quantum computer

by Thamarasee Jeewandara , Phys.org

Quantum chemistry simulations on a quantum computer
SO-QFT simulation of 2D hydrogenic electron. (A) Real projections of the ground ψ0,0 state (left) and a first excited ψ1,1 state (right) of 2D hydrogen. Note that the plots here do not reflect the choice of simulation box size and are not to scale. (B) Top represents difference between the energy from phase estimation and the analytic energy of 2D hydrogen. Bottom captures the deviation of the simulation fidelity at the end of the propagation. In this series of experiments, we initialized the ground state ψ0,0 centered in a simulation box with L = 10 a.u., such that the origin of the Coulomb singularity lies halfway between two central grid points. Each subregister has a budget of 8 ≤ nr ≤ 12 qubits to store the wave function, corresponding to spatial resolutions of 0.039 ≥ δr ≥ 0.002 a.u. We also initialize the ψ1,1 excited state in a simulation box with sides of length 40 a.u., with budgets of 7 ≤ nr ≤ 10 qubits per subregister and corresponding resolutions of 0.313 ≥ δr ≥ 0.039 a.u. These two states, represented at different spatial resolutions, are all time-propagated using the first-order SO for 1.5 atomic time units. We used time steps between 0.00001 ≤ δt ≤ 0.01 (150,000 to 150 SO steps) for the ψ0,0 state and between 0.001 ≤ δt ≤ 0.1 (1500 to 15 SO steps) for the ψ1,1 state. (C) The difference between the final and initial energy expectation value, measured by direct sampling of the state, of the ground state (left), and the first excited state (right), propagated at different spatial and time resolutions. The left inset plot zooms in on the energy error at high temporal resolutions for the ground state. Credit: Science Advances (2023). DOI: 10.1126/sciadv.abo7484

In a new report now featured on the cover page of and published in Science Advances, Hans Hon Sang Chan and a research team in materials, chemistry and quantum photonics at the University of Oxford generated exactly emulated quantum computers with up to 36 qubits to explore resource-frugal algorithms and model two- and three-dimensional atoms with single and paired particles.

Chemistry modeling is a natural attribute for quantum computers, although existing methods are impractical to develop near-perfect qubits. In this work, quantum chemists explored a range of tasks from ground state preparation and energy estimation to scattering and ionization dynamics of electrons, to assess a variety of methods in the split-operative simulation in order to emulate the of a few molecules of interest. The grid-based method performed exceptionally to make way for a less error-prone quantum computing era.

Quantum computing via a real-space grid approach

Quantum chemists envision quantum computers to be transformative tools for chemistry prediction and exploration. While conventional computers are useful to explore quantum molecular dynamics to predict reaction outcomes and experimental observables, the hardware costs and time duration can scale exponentially with the number of simulated particles. In this work, Chan and colleagues studied the underlying characteristics of accelerating chemical dynamics simulations on early versions of quantum computers based on a real-space grid approach.

These early versions of quantum computers had a limited number of error-corrected qubits. The team encoded features such as particle symmetry to offer optimal resource scaling for complex and interesting molecules during the study.

Most quantum computers are noise-burdened and costly. The researchers therefore took a different approach by deploying classical computing resources to emulate small, but noise-free quantum computers to thereby simulate quantum within them—to directly examine the costs and performance measures. While they did not rehash pre-existing classical-grid techniques to perform grid-based simulations, they conducted emulations of real, noise-free quantum machines for chemically relevant quantum dynamics instead.

Quantum chemistry simulations on a quantum computer
Preparing the ground state of 2D hydrogen using the PITE technique. The method was emulated on a 1 + 2 × 10–qubit quantum computer. Post-select the successful outcome at all times. The main plot shows the overlap of the propagated state with analytic eigenstates. Bottom shows scaled cross sections of the electron probability density sampled at labeled points during the imaginary-time evolution. Top right shows the same probability densities plotted on the same scale. Credit: Science Advances (2023). DOI: 10.1126/sciadv.abo7484

A new approach for quantum chemistry

The costs of mimicry limited the quantum computer-emulations to modest-sized versions containing 36 perfect qubits. The team used the experimental setup to explore several informative scenarios for 2D and 3D simulations of one- and two-electron systems. They selected two key areas of interest in chemistry, and estimated the requisite quantum resources to simulate the dynamics of strong external fields, followed by simulations of particle scattering dynamics.

During the first experiment, the team applied an external field suddenly with resulting dipole oscillation and ionization of a single bound electron. They envision efforts in this direction to encompass topics such as photochemistry and laser excitation. Physicists and quantum chemists consider coherent quantum regulation of small molecules to be one of the "holy grails" of chemical science. For example, the process can allow scientists to study ammonia in the context of hydrogen atom removal to explore its potential in modern agriculture.

In the second scenario, the team examined electron-molecule scattering relevant in spectroscopy, astrochemistry and manufacturing processes, since the processes of collision and scattering are highly dynamic and difficult for classical modeling.

Quantum chemistry simulations on a quantum computer
The performance of the ASO technique. The emulated quantum computer has 13 = 1 + 6 × 6 qubits. (A) The 3D inset depicts the eigenstate ψ0,0 of 2D hydrogen within its simulation box. The graph shows the autocorrelation of the state at time t with respect to the initial state, which ideally remains at unity (blue dashed line). The red, orange, and green lines are respectively the cases of no augmentation, a 2 × 2 augmentation, and a 4 × 4 augmentation. (B) The result of phase estimation for the same three cases, with the ideal again shown with a blue dashed line. The contour plots on the right show the absolute difference in probability density, with respect to the initial state, for the case of no augmentation (red) and the 2 × 2 augmentation (orange). (C) Generic circuit used. (D) and (E) specify the particular circuits used for our 2 × 2 and 4 × 4 augmentations, respectively. The A operators simply increment the indexing of the spatial "pixels" so that the bottom right pixel is (0,0). In the case of the 2 × 2 augmentation, the increment used is G = 1 so that A maps the indices of the pixels of interest, i.e., (−1,−1), (−1,0), (0,−1), and (0,0) to (0,0), (0,1), (1,0), and (1,1), respectively. These indices are now exactly those states for which the most important nr − 1 qubits are zero, facilitating the application of the small-augmentation circuit to only the four target states. Credit: Science Advances (2023). DOI: 10.1126/sciadv.abo7484

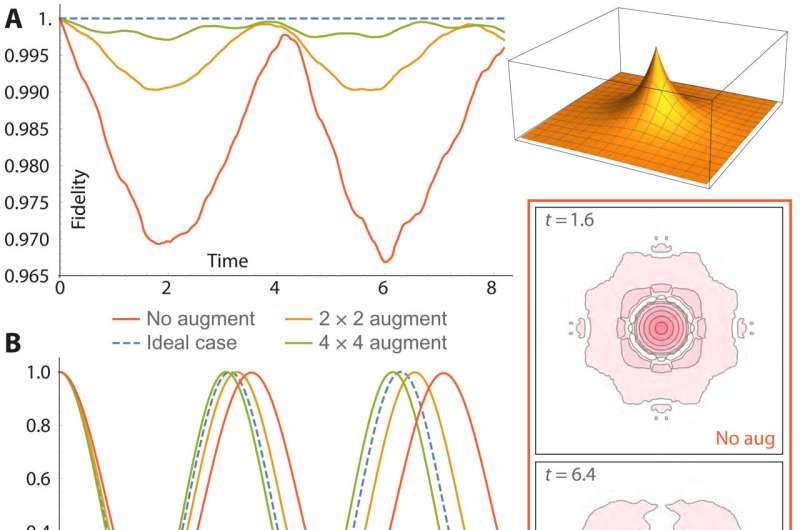
Wave simulation

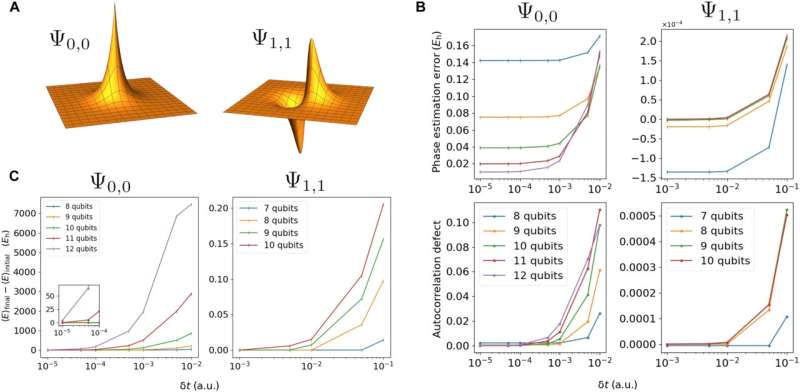
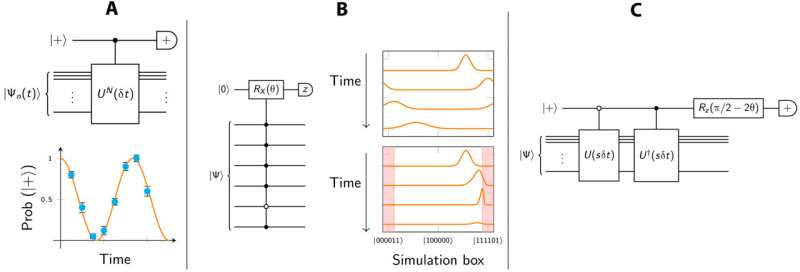
The scientists used the split-operator quantum Fourier transform (SO-QFT) Hamiltonian simulation approach to perform wave packet operations and presented a range of results that applied to the grid-based method for 2-to-3D systems using single and paired particles. Based on the outcomes, they assessed the quantum resources required for simulations, in order to present suitable quantum hardware architecture.

The numerical outcomes led to emulating quantum processors by implementing them via open-source tools such as QuEST, QuEST-link and pyQuEST. They explored the number of qubits and estimated the duration of execution to achieve simulations of given accuracy, and studied a scenario of a sampling-based method to estimate the system's energy, which proved to be highly sensitive to imperfections. They estimated the accompanying quantum resource costs and indicated the hardware layout for a suitable quantum computer.

Quantum chemistry simulations on a quantum computer
Simulation of a helium atom in real space. The top plot is the Bhattacharyya coefficient (with and without enabled electron-electron interactions), and the bottom is the real-space electron density distributions during the time evolution of the helium atom simulation. Colored shells are electron probability density isosurfaces, within a simulation box with L = 25 a.u. Distributions are shown for the initial state, at the time where it is maximally spread out, and at the end of the simulation. The 500 SO cycles correspond to the propagation of 25 a.u. (≈0.6 fs). Credit: Science Advances (2023). DOI: 10.1126/sciadv.abo7484

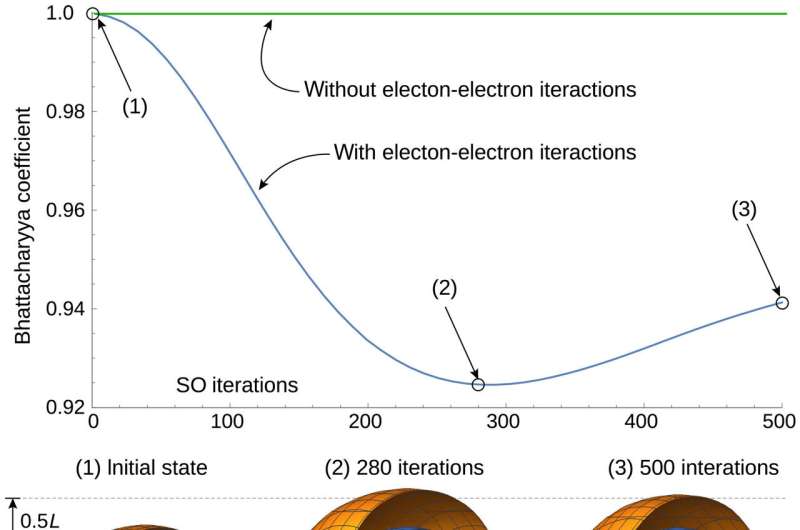
Methods and 3D simulations

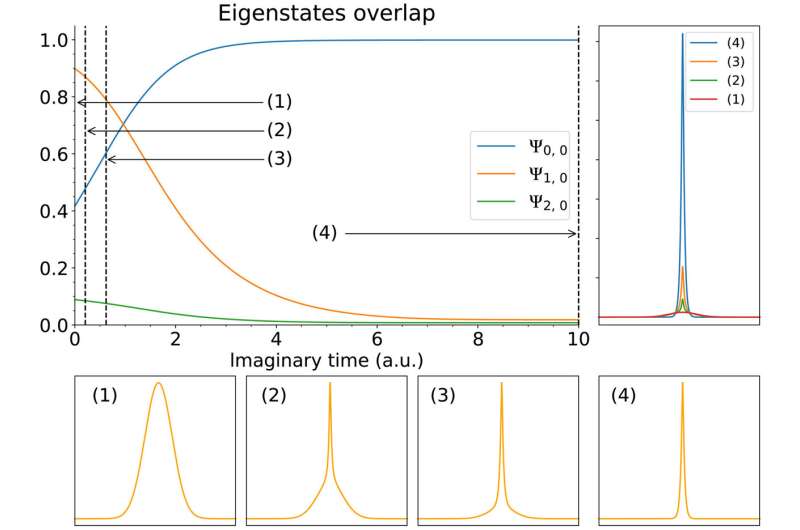
The research team explored single-ancilla iterative phase estimation (IPE) measurements to project out excited states. The IPE circuits are interesting and important for near-term quantum computing in practice. The results served for energy estimation and the team conducted alternative approaches to prepare real-space ground states on a quantum computer based on probabilistic imaginary time evolution (PITE) and simulated the ground state of 2D hydrogen, while detailing drawbacks of the method. They carried out two scenarios of quantum dynamics simulations that relied on two scenarios 1) ionization by a strong external field, and 2) dependence on electron-electron scattering.

The team next introduced the augmented split-operator (ASO) to optimize the fidelity of the simulation by presenting additional elements to the basic SO-QFT (split-operator quantum Fourier transform) cycle. When operating with strict Coulomb interactions common to all numerical studies as seen in this paper, the ASO method was highly relevant. Using the setup, they simulated the dynamics of a helium atom in 3D. They used the Schrodinger equation to approximate the true electron eigenstates of the helium atom, and the Bhattacharya coefficient to represent electron-electron interactions and time evolution of the helium atom simulation.

Quantum chemistry simulations on a quantum computer
A possible "multicore" architecture. On the basis of distributing the P particle state over P/2 memory nodes (3nr qubits) and P/2 compute nodes (6nr qubits), which are interlinked either on-chip or at the macroscale. Top right indicates that three steps occur in a compute node. In step 1, quantum addition and subtraction are used to move to the relative and total coordinates (and step 3 will reverse this). In the middle, step 2, the relative coordinate is used to apply phase shifts required by the SO cycle, and optionally, we apply an augmentation step. Bottom shows how parallelized phases alternatingly process and permute the data. The numbers within the circles and squares are the labels of particles; they correspond to the subscripts of the x, y, and z symbols on the top right. Credit: Science Advances (2023). DOI: 10.1126/sciadv.abo7484

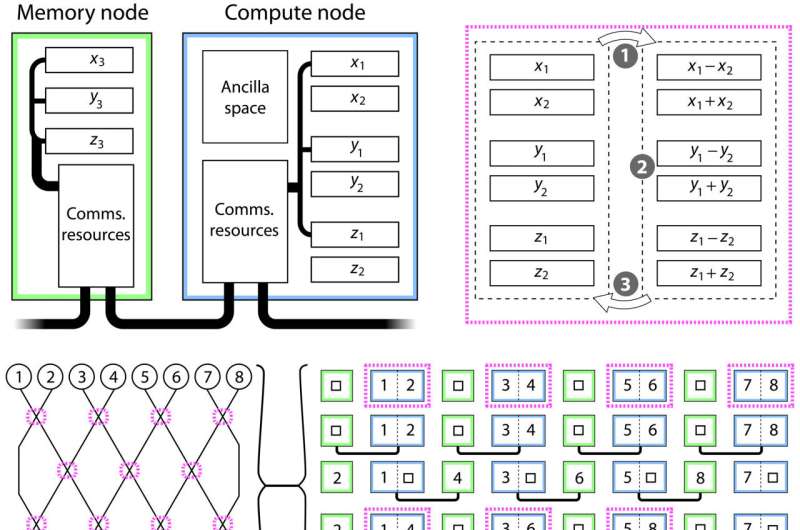
Quantum computing resources and architectures

The quantum chemists studied the resource requirements to undertake quantum modeling beyond the reach of classical algorithms, and aligned quantum architectures suited for such expressions. They estimated the number of qubits necessary to model quantum scenarios of interest for hexafluoro ethane (C2F6) and ammonia (NH3) molecules. The grid-based simulations of C2F6 required about 2250 computational qubits, while the ammonia molecules required less than 450 qubits.

The time cost for simulation also relied on hardware realization. As a result, the most well-understood codes required many hundreds of physical qubits per logical qubit relative to deep algorithms and error-rates, comparable to the best quantum computer prototypes of today. The researchers additionally devised a multicore network architecture to support the theoretical massive-scale qubits.

Quantum chemistry simulations on a quantum computer
Three early fault-tolerant quantum circuit techniques for real-space chemistry explored in this work. (A) The single-ancilla IPE method emulated in this work. The global phase is encoded in the probability of measuring an entangled ancilla qubit, which controls the application of N SO cycles, in the ∣+⟩ state. To obtain this probability, one must repeat the propagation and measurement at each point in time where one wishes to sample the signal. (B) Attenuation of a wave packet on a qubit register. Top right depicts the dispersion of a Gaussian wave packet across the periodic boundary. Addition of complex absorbing region in pink (bottom right) attenuates the scattered wave packet by reducing its norm. In the illustrated case, the process is not quite perfect: There is some reflection caused by the attenuation being too severe. Left is a circuit that performs probabilistic wave packet attenuation at a select pixel. The pixel ∣111101⟩ is selected, corresponding to the attenuating region on the right-hand side of the simulation box in the figure. (C) Preparing ground states using the PITE circuit. The filled circles indicate "control by ∣1⟩," and the open circles indicate "control by 0." Post-selecting on the ∣+⟩ outcome yields a state with, to first order, an imaginary-time evolution step applied. Credit: Science Advances (2023). DOI: 10.1126/sciadv.abo7484

Outlook

In this way, Hans Hon Sang Chan and colleagues explored the split-operator quantum Fourier transform (SO-QFT) approach to emulate exact qubits and test the technologies behind real-space quantum chemistry simulations. They explored several known quantum techniques and introduced a few others to convey key aspects of quantum . The scientists characterized the resources underlying the realization of digital experiments on early fault-tolerant quantum computers.

The outcomes can be a learning/prediction cycle by augmenting physical experiments with machine learning to accelerate chemical discovery. The results can lead to diverse fields of quantum technology, including special relativity to model high energy particles as well as play a role in financial engineering.

More information: Hans Hon Sang Chan et al, Grid-based methods for chemistry simulations on a quantum computer, Science Advances (2023). DOI: 10.1126/sciadv.abo7484

Chris Sparrow et al, Simulating the vibrational quantum dynamics of molecules using photonics, Nature (2018). DOI: 10.1038/s41586-018-0152-9

Journal information: Science Advances , Nature

© 2023 Science X Network

Citation: Quantum chemistry simulations on a quantum computer (2023, March 14) retrieved 26 March 2023 from https://phys.org/news/2023-03-quantum-chemistry-simulations.html
This document is subject to copyright. Apart from any fair dealing for the purpose of private study or research, no part may be reproduced without the written permission. The content is provided for information purposes only.

Explore further

Quantum algorithms save time in the calculation of electron dynamics
349 shares

Feedback to editors
Load comments (0)