Feeling out of equilibrium in a dual geometric world: A novel theory for nonlinear dissipative phenomena

Losing energy is rarely a good thing, but now, researchers in Japan have shown how to extend the applicability of thermodynamics to systems that are not in equilibrium. By encoding the energy dissipation relationships in a geometric way, they were able to cast the physical constraints in a generalized geometric space. This work may significantly improve our understanding of chemical reaction networks, including those that underlie the metabolism and growth of living organisms.

Thermodynamics is the branch of physics dealing with the processes by which energy is transferred between entities. Its predictions are crucial for both chemistry and biology when determining if certain chemical reactions, or interconnected networks of reactions, will proceed spontaneously. However, while thermodynamics tries to establish a general description of macroscopic systems, often we encounter difficulties in working on the system out of equilibrium. Successful attempts to extend the framework to nonequilibrium situations have usually been limited only to specific systems and models.

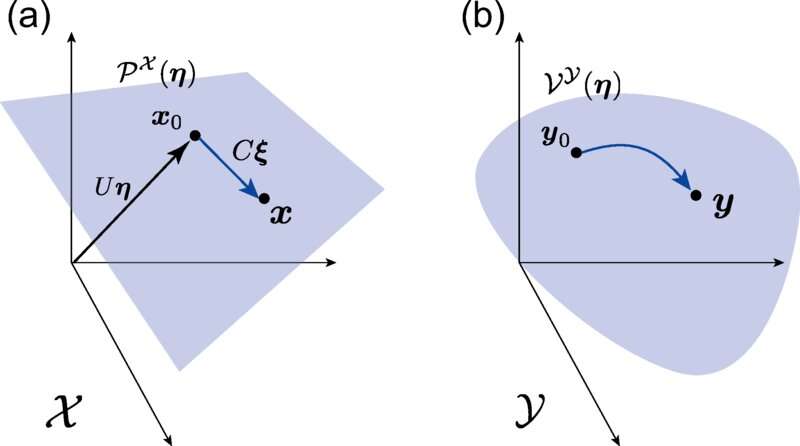
In two recently published studies in Physical Review Research, researchers from the Institute of Industrial Science at The University of Tokyo demonstrated that complex nonlinear chemical reaction processes could be described by transforming the problem into a geometrical dual representation. "With our structure, we can extend theories of nonequilibrium systems with quadratic dissipation functions to more general cases, which are important for studying chemical reaction networks," says first author Tetsuya J. Kobayashi.

In physics, duality is a central concept. Some physical entities are easier to interpret when transformed into a different, but mathematically equivalent, representation. As an example, a wave in the time space can be transformed into its representation in the frequency space, which is its dual form. When dealing with chemical processes, thermodynamic force and flux are the nonlinearly related dual representations—their product leads to the rate at which energy is lost to dissipation—in a geometric space induced by the duality, the scientists were able to show how thermodynamic relationships can be generalized even in nonequilibrium cases.

"Most previous studies of chemical reaction networks relied on assumptions about the kinetics of the system. We showed how they can be handled more generally in the nonequilibrium case by employing the duality and associated geometry," says last author Yuki Sughiyama. Possessing a more universal understanding of thermodynamic systems, and extending the applicability of nonequilibrium thermodynamics to more disciplines, can provide a better vantage point for analyzing or designing complex reaction networks, such as those used in living organisms or industrial manufacturing processes.