Deep learning from a dynamical viewpoint

NUS mathematicians have developed a new theoretical framework based on dynamical systems to understand when and how a deep neural network can learn arbitrary relationships.

Despite achieving widespread success in practice, understanding the theoretical principles of deep learning remains a challenging task. One of the most fundamental questions is: can deep neural networks learn arbitrary input-output relationships (in mathematics, these are called functions), and does the way they achieve this differ from traditional methodologies?

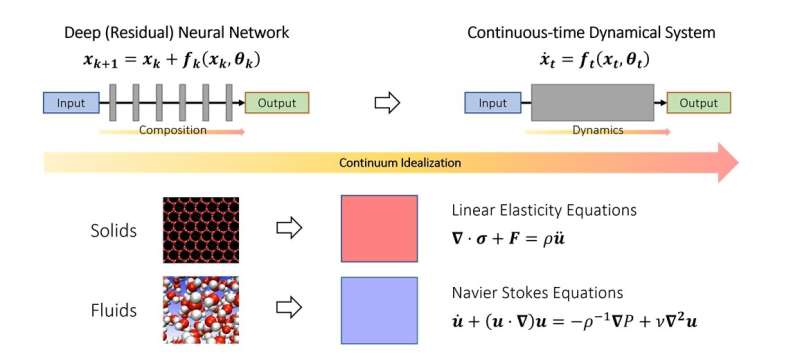
To understand this question, it is necessary to think about what exactly is new in deep neural networks compared to traditional function approximation paradigms. For example, classical Fourier series approximates complicated functions as a weighted sum of simpler functions, such as sines and cosines. Deep neural networks operate quite differently. Instead of weighted sums, they build complex functions out of the repeated stacking of simple functions (layers). This is also known as function composition in mathematics. The key question is how complicated functions can be built out of simple ones by stacking them together. It turns out that this is quite a new problem in the branch of mathematics known as approximation theory.

In this study published in the Journal of the European Mathematical Society, Assistant Professor Qianxiao LI from the Department of Mathematics, National University of Singapore and his collaborators developed a new theory of approximation capabilities of function composition. An interesting observation is that while function composition is challenging to analyze in practice due to its discrete and nonlinear structure, this is not the first time there are such problems.

In the study of the motion of solids and fluids, they are often idealized as a continuum of particles, satisfying some continuous equations (ordinary or partial differential equations). This allows the difficulty of modeling such systems at the discrete, atomic level to be circumvented. Instead, continuum equations that model their behavior at the macroscopic level were derived.

The key idea in the study is that this concept can be extended to deep neural networks, by idealizing the layered structure as a continuous dynamical system. This connects deep learning with the branch of mathematics known as dynamical systems. Such connections allow for the development of new tools to understand the mathematics of deep learning, including a general characterization of when it can indeed approximate arbitrary relationships.

Prof Li said, "The dynamical systems viewpoint of deep learning offers a promising mathematical framework that highlights the distinguishing aspects of deep neural networks compared with traditional paradigms. This brings exciting new mathematical problems on the interface of dynamical systems, approximation theory and machine learning."

"A promising area of future development is to extend this framework to study other aspects of deep neural networks, such as how to train them effectively and how to ensure they work better on unseen datasets," added Prof Li.