Theoretical model describing the motion of ultrasound waves in the presence of multiple bubbles
Scientists from the Graduate School of Systems and Information Engineering at the University of Tsukuba created a theoretical model for describing the motion of ultrasound waves in the presence of multiple bubbles. This work may assist doctors in designing new diagnostic and therapeutic applications of ultrasound technology.
Focused ultrasound medical treatments for ablating tumors or breaking up kidney stones with shock wave lithotripsy can offer the chance for improved patient outcomes without exposure to electromagnetic or particle radiation. However, these methods rely on an understanding of the way ultrasound waves move through complex environments, such as living tissue. This is especially true for tumor ablation therapy, which works by directing the heat created from the ultrasound to destroy diseased cells. More complete wave propagation equations are needed to ensure these modalities are being implemented correctly.
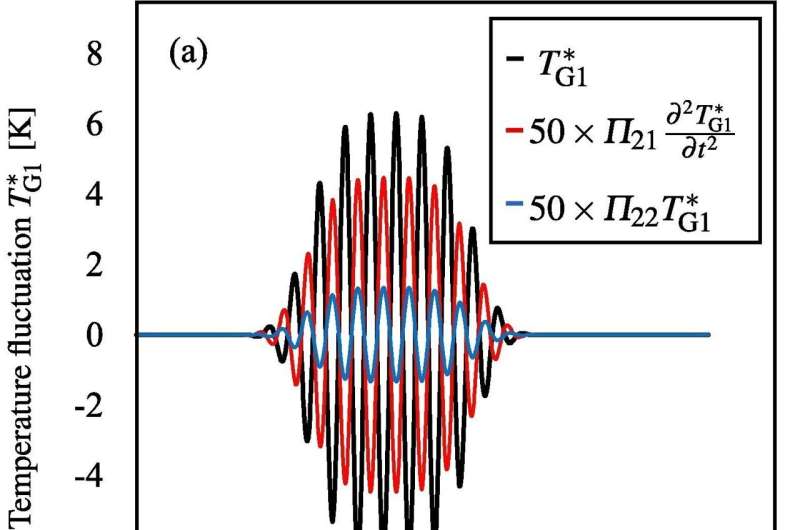
Now, scientists at the University of Tsukuba have extended the conventional model of sound wave propagation to include multiple bubbles. The Khokhlov—Zabolotskaya—Kuznetsov (KZK) equation has previously been used as a simplified model for the nonlinear propagation of focused ultrasound in a pure liquid. Being able to write a single equation to model nonlinear ultrasound, bubble oscillations, and temperature fluctuation in a consistent manner opens the way toward microbubble-enhanced medical applications.
"A mathematical model for medical applications utilizing bubbles should describe the nonlinearity of both ultrasound propagation and bubble oscillation," says author Professor Tetsuya Kanagawa. The scientists used a method of combining multiple sizes scales by computing the volumetric averaged basic equations for bubbly liquids. The resulting equations had terms for nonlinear effects, sound dissipation, dispersion, and focusing. In particular, the dissipation term itself depended on three factors: interfacial liquid viscosity, liquid compressibility and the thermal conductivity of gas inside bubbles.
"In future refinements, we can add theoretical extensions of the KZK equation that incorporate the viscous effects of bulk liquid, the elasticity of body tissues, and heat transfer," says Professor Kanagawa. One early application is the use of microbubbles as contrast agents for improving the resolution of ultrasound images. However, they may also be extended to interventions that accomplish the targeted ablation of tissues.
More information: Shunsuke Kagami et al, Weakly nonlinear propagation of focused ultrasound in bubbly liquids with a thermal effect: Derivation of two cases of Khokolov–Zabolotskaya–Kuznetsoz equations, Ultrasonics Sonochemistry (2022). DOI: 10.1016/j.ultsonch.2022.105911
Provided by University of Tsukuba