Tear-free brushing? All you need is math
As anyone who has ever had to brush long hair knows, knots are a nightmare. But with enough experience, most learn the tricks of detangling with the least amount of pain—start at the bottom, work your way up to the scalp with short, gentle brushes, and apply detangler when necessary.
L. Mahadevan, the Lola England de Valpine Professor of Applied Mathematics, of Organismic and Evolutionary Biology, and of Physics, learned the mechanics of combing years ago while brushing his young daughter's hair.
"I recall that detangling spray seemed to work sometimes, but I still had to be careful to comb gently, by starting from the free ends," said Mahadevan. "But I was soon fired from the job as I was not very patient."
While Mahadevan lost his role as hairdresser, he was still a scientist and the topology, geometry and mechanics of detangling posed interesting mathematical questions that are relevant to a range of applications including textile manufacturing and chemical processes such as polymer processing.
In a new paper, published in the journal Soft Matter, Mahadevan and co-authors Thomas Plumb Reyes and Nicholas Charles, explore the mathematics of combing and explain why the brushing technique used by so many is the most effective method to detangle a bundle of fibers.
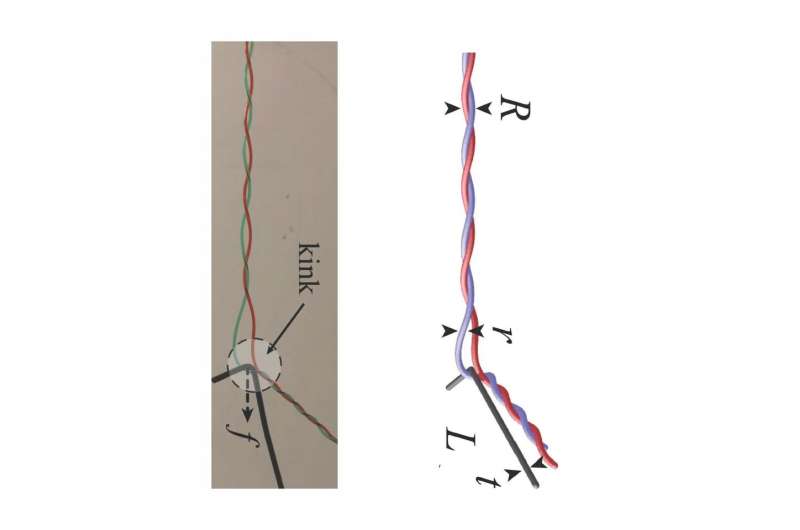
To simplify the problem, the researchers simulated two helically entwined filaments, rather than a whole head of hair.
"Using this minimal model, we study the detangling of the double helix via a single stiff tine that moves along it, leaving two untangled filaments in its wake," said Plumb-Reyes, a graduate student at SEAS. "We measured the forces and deformations associated with combing and then simulated it numerically."
"Short strokes that start at the free end and move towards the clamped end remove tangles by creating a flow of a mathematical quantity called the 'link density' that characterizes the amount that hair strands that are braided with each other, consistent with simulations of the process," said Nicholas Charles, a graduate student at SEAS.
The researchers also identified the optimal minimum length for each stroke—any smaller and it would take forever to comb out all the tangles and any longer and it would be too painful.
The mathematical principles of brushing developed by Plumb-Reyes, Charles and Mahadevan were recently used by Professor Daniela Rus and her team at MIT to design algorithms for brushing hair by a robot.
Next, the team aims to study the mechanics of brushing curlier hair and how it responds to humidity and temperature, which may lead to a mathematical understanding of a fact every person with curly hair knows: never brush dry hair.
More information: Thomas B. Plumb-Reyes et al, Combing a double helix, Soft Matter (2022). DOI: 10.1039/D1SM01533H
Journal information: Soft Matter