Quantum theory needs complex numbers

Physicists construct theories to describe nature. Let us explain it through an analogy with something that we can do in our everyday life, like going on a hike in the mountains. To avoid getting lost, we generally use a map. The map is a representation of the mountain, with its houses, rivers, paths, etc. By using it, it is rather easy to find our way to the top of the mountain. But the map is not the mountain. The map constitutes the theory we use to represent the mountain's reality.
Physical theories are expressed in terms of mathematical objects, such as equations, integrals or derivatives. During history, physics theories evolved, making use of more elaborate mathematical concepts to describe more complicated physics phenomena. Introduced in the early 20th century to represent the microscopic world, the advent of quantum theory was a game changer. Among the many drastic changes it brought, it was the first theory phrased in terms of complex numbers.
Invented by mathematicians centuries ago, complex numbers are made of a real and imaginary part. It was Descartes, the famous philosopher considered as the father of rational sciences, who coined the term "imaginary," to strongly contrast it with what he called "real" numbers. Despite their fundamental role in mathematics, complex numbers were not expected to have a similar role in physics because of this imaginary part. And in fact, before quantum theory, Newton's mechanics or Maxwell's electromagnetism used real numbers to describe, say, how objects move, as well as how electro-magnetic fields propagate. The theories sometimes employ complex numbers to simplify some calculations, but their axioms only make use of real numbers.
Schrödinger's bewilderment
Quantum theory radically challenged this state of affairs because its building postulates were phrased in terms of complex numbers. The new theory, even if very useful for predicting the results of experiments, and for instance perfectly explains the hydrogen atom energy levels, went against the intuition in favor of real numbers. Looking for a description of electrons, Schrödinger was the first to introduce complex numbers in quantum theory through his famous equation. However, he could not conceive that complex numbers could actually be necessary in physics at that fundamental level. It was as though he had found a map to represent the mountains but this map was actually made out of abstract and non-intuitive drawings. Such was his bewilderment that he wrote a letter to Lorentz on June 6, 1926, stating "What is unpleasant here, and indeed directly to be objected to, is the use of complex numbers. Ψ is surely fundamentally a real function." Several decades later, in 1960, Prof. E.C.G. Stueckelberg, from the University of Geneva, demonstrated that all predictions of quantum theory for single-particle experiments could equally be derived using only real numbers. Since then, the consensus was that complex numbers in quantum theory were only a convenient tool.
However, in a recent study published in Nature, ICFO researchers Marc-Olivier Renou and ICREA Prof. at ICFO Antonio Acín, in collaboration with Prof. Nicolas Gisin from the University of Geneva and the Schaffhausen Institute of Technology, Armin Tavakoli from the Vienna University of Technology, and David Trillo, Mirjam Weilenmann, and Thinh P. Le, led by Prof. Miguel Navascués, from the Institute of Quantum Optics and Quantum Information (IQOQI) of the Austrian Academy of Sciences in Vienna have proven that if the quantum postulates were phrased in terms of real numbers, instead of complex, then some predictions about quantum networks would necessarily differ. Indeed, the team of researchers came up with a concrete experimental proposal involving three parties connected by two sources of particles where the prediction by standard complex quantum theory cannot be expressed by its real counterpart.
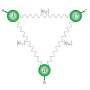
Two sources and three nodes
To do this, they thought of a specific scenario that involves two independent sources (S and R), placed between three measurement nodes (A, B and C) in an elementary quantum network. The source S emits two particles, say photons, one to A, and the second to B. The two photons are prepared in an entangled state, say in polarization. That is, they have correlated polarization in a way which is allowed by (both complex and real) quantum theory but impossible classically. The source R does exactly the same, emits two other photons prepared in an entangled state and sends them to B and to C, respectively. The key point in this study was to find the appropriate way to measure these four photons in the nodes A, B, C in order to obtain predictions which cannot be explained when quantum theory is restricted to real numbers.
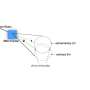
As ICFO researcher Marc-Olivier Renou comments "When we found this result, the challenge was to see if our thought experiment could be done with current technologies. After discussing with colleagues from Shenzhen-China, we found a way to adapt our protocol to make it feasible with their state-of-the-art devices. And, as expected, the experimental results match the predictions." This remarkable experiment, realized in collaboration with Zheng-Da Li, Ya-Li Mao, Hu Chen, Lixin Feng, Sheng-Jun Yang, Jingyun Fan from the Southern University of Science and Technology, and Zizhu Wang from the University of Electronic Science and Technology is published at the same time as the Nature paper in Physical Review Letters.
The results published in Nature can be seen as a generalization of Bell's theorem, which provides a quantum experiment which cannot be explained by any local physics formalism. Bell's experiment involves one quantum source S that emits two entangled photons, one to A, and the second to B, prepared in an entangled state. Here, in contrast, one needs two independent sources, the assumed independence is crucial and was carefully designed in the experiment.
The study also shows how outstanding predictions can be when combining the concept of a quantum network with Bell's ideas. For sure, the tools developed to obtain this first result are such that they will allow physicists to achieve a better understanding of quantum theory, and will one day trigger the realization and materialization of so far unfathomable applications for the quantum internet.
More information: Miguel Navascués, Quantum theory based on real numbers can be experimentally falsified, Nature (2021). DOI: 10.1038/s41586-021-04160-4. www.nature.com/articles/s41586-021-04160-4
Journal information: Nature , Physical Review Letters
Provided by ICFO