Random close packing or jamming of spheres in a container

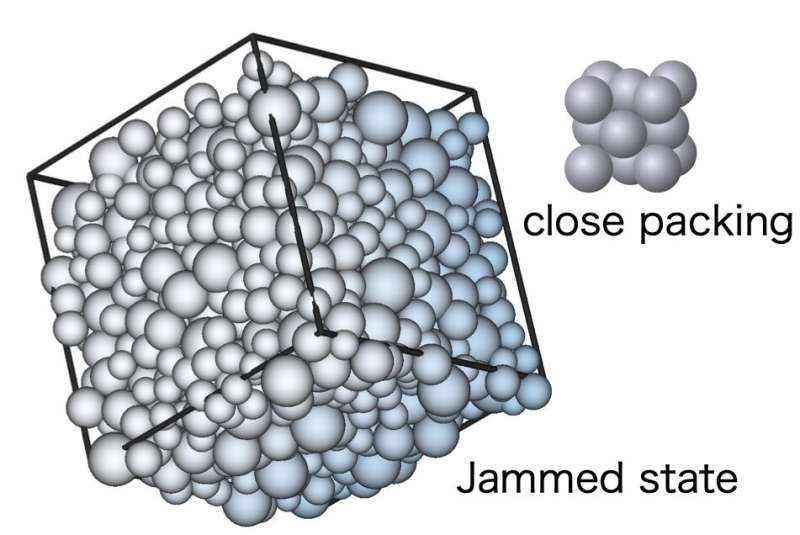
Scientists at the theoretical institutes, Chinese Academy of Science and Cybermedia Center at Osaka University performed extensive computer simulations to generate and examine random packing of spheres. They show that the "jamming" transition, in which a free-flowing material becomes stuck, occurs with universal features despite the diversity of their details. This work may shed light on the physics of amorphous materials and optimization problems in computer science which are intimately related to the mathematics of sphere packings.

How many oranges can fit in a spherical bowl? This seemingly prosaic question actually leads to a fascinating topic of efficient packing theory and the concept of "jamming." While it is known that spheres can be packed regularly to take up a maximum of 74% of the volume, the corresponding limit for random packings is thought to be around 64%, but this has not been proved. The solution is related to the ability of certain soft matter materials, including sand, colloid, foam, or polymers to become jammed by compression or shear. You can experiment for yourself using a box of cereal that will suddenly stop pouring.

Now, the team used simulated collections of frictionless spheres on supercomputers and found that jammed states can be obtained either by compression or by shear in a broad range of densities larger than 64% and with a broad range of anisotropies. They found, the diverse jammed states are all at the verge of mechanical stability and exhibit the same critical properties. "We demonstrated that compression and shear-jammed frictionless packings can be described under a unified framework," first author Yuliang Jin says. This implies the marginal stability is the robust, key mechanism which underlies jamming.

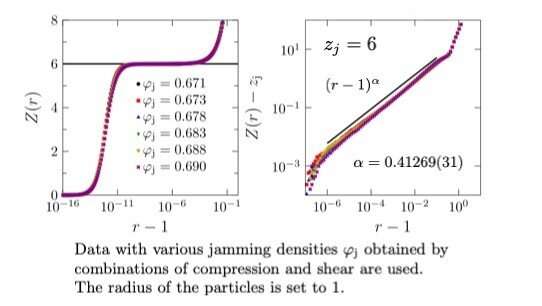
In this research, the coordination number refers to the number of neighbors a sphere has. The team showed that plots of the coordination number at various distances collapse onto the same curve regardless of particle density of the jammed states. "The densest packing of spheres represents a unique structure. Conversely, random packing, as with the atoms in a glass, can lead to arrangements with various densities depending on the method of compression and shear applied," senior author Hajime Yoshino says. This research, which sheds light on the efficient packing of solid objects, may lead to new ideas for the industrial production of glasses, foams, and other jammable materials.