Lack of symmetry in qubits can't fix errors in quantum computing, might explain matter/antimatter
A team of quantum theorists seeking to cure a basic problem with quantum annealing computers—they have to run at a relatively slow pace to operate properly—found something intriguing instead. While probing how quantum annealers perform when operated faster than desired, the team unexpectedly discovered a new effect that may account for the imbalanced distribution of matter and antimatter in the universe and a novel approach to separating isotopes.
"Although our discovery did not the cure the annealing time restriction, it brought a class of new physics problems that can now be studied with quantum annealers without requiring they be too slow," said Nikolai Sinitsyn, a theoretical physicist at Los Alamos National Laboratory. Sinitsyn is author of the paper published Feb. 19 in Physical Review Letters, with coauthors Bin Yan and Wojciech Zurek, both also of Los Alamos, and Vladimir Chernyak of Wayne State University.
Significantly, this finding hints at how at least two famous scientific problems may be resolved in the future. The first one is the apparent asymmetry between matter and antimatter in the universe.
"We believe that small modifications to recent experiments with quantum annealing of interacting qubits made of ultracold atoms across phase transitions will be sufficient to demonstrate our effect," Sinitsyn said.
Explaining the matter/antimatter discrepancy
Both matter and antimatter resulted from the energy excitations that were produced at the birth of the universe. The symmetry between how matter and antimatter interact was broken but very weakly. It is still not completely clear how this subtle difference could lead to the large observed domination of matter compared to antimatter at the cosmological scale.
The newly discovered effect demonstrates that such an asymmetry is physically possible. It happens when a large quantum system passes through a phase transition, that is, a very sharp rearrangement of quantum state. In such circumstances, strong but symmetric interactions roughly compensate each other. Then subtle, lingering differences can play the decisive role.
Making quantum annealers slow enough
Quantum annealing computers are built to solve complex optimization problems by associating variables with quantum states or qubits. Unlike a classical computer's binary bits, which can only be in a state, or value, of 0 or 1, qubits can be in a quantum superposition of in-between values. That's where all quantum computers derive their awesome, if still largely unexploited, powers.
In a quantum annealing computer, the qubits are initially prepared in a simple lowest energy state by applying a strong external magnetic field. This field is then slowly switched off, while the interactions between the qubits are slowly switched on.
"Ideally an annealer runs slow enough to run with minimal errors, but because of decoherence, one has to run the annealer faster," Yan explained. The team studied the emerging effect when the annealers are operated at a faster speed, which limits them to a finite operation time.
"According to the adiabatic theorem in quantum mechanics, if all changes are very slow, so-called adiabatically slow, then the qubits must always remain in their lowest energy state," Sinitsyn said. "Hence, when we finally measure them, we find the desired configuration of 0s and 1s that minimizes the function of interest, which would be impossible to get with a modern classical computer."
Hobbled by decoherence
However, currently available quantum annealers, like all quantum computers so far, are hobbled by their qubits' interactions with the surrounding environment, which causes decoherence. Those interactions restrict the purely quantum behavior of qubits to about one millionth of a second. In that timeframe, computations have to be fast—nonadiabatic—and unwanted energy excitations alter the quantum state, introducing inevitable computational mistakes.
The Kibble-Zurek theory, co-developed by Wojciech Zurek, predicts that the most errors occur when the qubits encounter a phase transition, that is, a very sharp rearrangement of their collective quantum state.
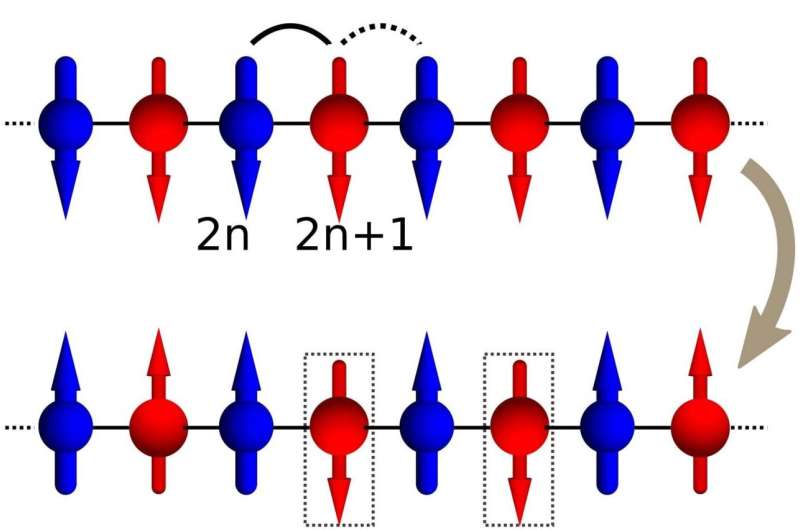
For this paper, the team studied a known solvable model where identical qubits interact only with their neighbors along a chain; the model verifies the Kibble-Zurek theory analytically. In the theorists' quest to cure limited operation time in quantum annealing computers, they increased the complexity of that model by assuming that the qubits could be partitioned into two groups with identical interactions within each group but slightly different interactions for qubits from the different groups.
In such a mixture, they discovered an unusual effect: One group still produced a large amount of energy excitations during the passage through a phase transition, but the other group remained in the energy minimum as if the system did not experience a phase transition at all.
"The model we used is highly symmetric in order to be solvable, and we found a way to extend the model, breaking this symmetry and still solving it," Sinitsyn explained. "Then we found that the Kibble-Zurek theory survived but with a twist—half of the qubits did not dissipate energy and behaved 'nicely.' In other words, they maintained their ground states."
Unfortunately, the other half of the qubits did produce many computational errors—thus, no cure so far for a passage through a phase transition in quantum annealing computers.
A new way to separate isotopes
Another long-standing problem that can benefit from this effect is isotope separation. For instance, natural uranium often must be separated into the enriched and depleted isotopes, so the enriched uranium can be used for nuclear power or national security purposes. The current separation process is costly and energy intensive. The discovered effect means that by making a mixture of interacting ultra-cold atoms pass dynamically through a quantum phase transition, different isotopes can be selectively excited or not and then separated using available magnetic deflection technique.
More information: Bin Yan et al, Nonadiabatic Phase Transition with Broken Chiral Symmetry, Physical Review Letters (2021). DOI: 10.1103/PhysRevLett.126.070602
Journal information: Physical Review Letters
Provided by Los Alamos National Laboratory