How complex oscillations in a quantum system simplify with time
Quantum physics allows to make statements about the behavior of a wide variety of many-particle systems at the atomic level, from salt crystals to neutron stars. In quantum systems, many parameters do not have concrete values, but are distributed over various values with certain probabilities. Often this distribution takes the form of a simple Gaussian bell curve that is encountered also in classical systems for example the distribution of balls in the Galton box experiment. However, not all quantum systems follow this simple behavior and some might deviate from the Gaussian distribution due to interactions.
Prof. Dr. Jens Eisert, who heads a joint research group on theoretical physics at the Freie Universität Berlin and the Helmholtz-Zentrum Berlin, argues that once interactions are reduced such deviations decay over time and become Gaussian distributed. Now he has been able to substantiate this presumption experimentally.
To do this, the Berlin team worked together with a group of experimental physicists led by Prof. Dr. Jörg Schmiedmayer at the Vienna University of Technology. Schmiedmayer and members of his group, in particular Dr. Thomas Schweigler, prepared a so-called Bose-Einstein condensate: this is a quantum system consisting of several thousand rubidium atoms, which were confined in a quasi-one-dimensional configuration with the help of magnetic fields and cooled near absolute zero (50 nanokelvin).
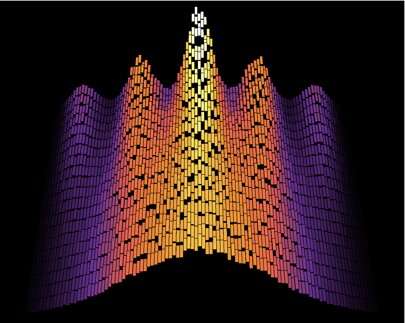
"The Vienna group created a synthetic quantum system in which the distribution of the phonons can be observed particularly sharply," explains Dr. Marek Gluza, coauthor of the study and postdoc with Jens Eisert. The measurement data initially represent the complex dynamics of the phonons. But the complexity is lost over time and the distribution takes on the shape of a Gaussian bell curve.
"In fact, we can see here how a Gaussian distribution emerges over time. Nature finds a simple solution, all by itself, through its physical laws," comments Jens Eisert.
What is unique about the performed experiment is that as time goes on the system swings back to the more complex distribution, demonstrating that the signatures of a complicated state can be retrieved again. "We know precisely why it swings back and what it depends on," Gluza explains. "This shows us something about the isolation of the system because the information about the signatures has never left the system."
More information: Thomas Schweigler et al, Decay and recurrence of non-Gaussian correlations in a quantum many-body system, Nature Physics (2021). DOI: 10.1038/s41567-020-01139-2
Journal information: Nature Physics
Provided by Helmholtz-Zentrum Berlin für Materialien und Energie