Rethinking a century of fluid flows

In 1922, English meteorologist Lewis Fry Richardson published Weather Prediction by Numerical Analysis. This influential work included a few pages devoted to a phenomenological model that described the way that multiple fluids (gases and liquids) flow through a porous-medium system and how the model could be used in weather prediction.
Since then, researchers have continued to build on and expand Richardson's model, and its principles have been used in fields such as petroleum and environmental engineering, hydrology, and soil science.
Cass Miller and William Gray, professors at the University of North Carolina at Chapel Hill, are two such researchers working together to develop a more complete and accurate method of fluid flow modeling.
Through a US Department of Energy (DOE) INCITE award, Miller and his team have been granted access to the IBM AC922 Summit supercomputer at the Oak Ridge Leadership Computing Facility (OLCF), a DOE Office of Science User Facility located at DOE's Oak Ridge National Laboratory (ORNL). The sheer power of the 200-petaflop machine means Miller can approach the subject of two-fluid flows (mixtures of liquids or gases) in a way that would have been inconceivable in Richardson's time.
Breaking tradition
Miller's work focuses on the way that two-fluid flows through porous media (rocks or wood, for example) are calculated and modeled. Numerous factors influence the movement of fluids through porous media, but for differing reasons, not all computational approaches consider them. In general, the basic phenomena that affect the transport of these fluids—such as the transfer of mass and momentum—are well-understood by researchers at a small scale and can be calculated accurately.
"If you look at a porous-media system at a smaller scale," Miller said, "a continuum scale where say, for example, a point exists entirely within one fluid phase or within a solid phase, we understand transport phenomena on that scale relatively well—we call that the microscale. Unfortunately, we can't solve very many problems at the microscale. As soon as you start thinking about where the solid particles are and where each fluid is, it becomes computationally and pragmatically overwhelming to describe a system at that scale."
To resolve this scale issue, researchers have traditionally approached most practical fluid flow problems at the macroscale, a scale at which computation becomes more feasible. Because numerous real-world applications require answers to multiple fluid flow problems, scientists have had to sacrifice certain details in their models for the purpose of accessible solutions. Further, Richardson's phenomenological model was written down with no formal derivation at the larger scale, meaning that fundamental microscale physics, for example, are not represented explicitly in traditional macroscale models.
In Richardson's day, these omissions were sensible. Without modern computational methods, linking microscale physics to a large-scale model was a nearly unthinkable task. But now, with help from the fastest supercomputer in the world for open science, Miller and his team are bridging the divide between the microscale and macroscale. To do so, they have developed an approach known as Thermodynamically Constrained Averaging Theory (TCAT).
"The idea of TCAT is to overcome these limitations," Miller said. "Can we somehow start from physics that are well or better understood and get to models that describe the physics for the systems that we're interested in at the macroscale?"
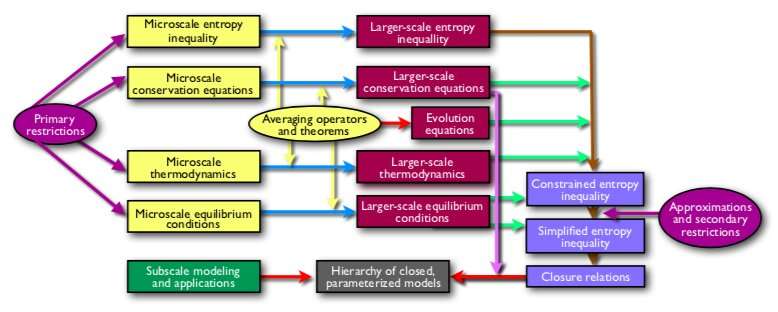
The TCAT approach
Physics at the microscale provides a fundamental groundwork for representing transport phenomena through porous media systems. To solve problems that are of interest to society, however, Miller's team needed to find a way to translate these first principles into large-scale mathematical models.
"The idea behind the TCAT model is that we start from the microscale," Miller said, "and we take that smaller-scale physics, which includes thermodynamics and conservation principles, and we move all of that up to the larger scale in a rigorous mathematical fashion where, out of necessity, we have to apply these models.
Miller's team uses Summit to help understand the detailed physics acting at the microscale and uses the results to help validate the TCAT model.
"We want to evaluate this new theory by pulling it apart and looking at individual mechanisms and by looking at larger systems and the overall model," Miller said. "The way that we do that is computation on a small scale. We routinely do simulations on lattices that can have up to billions of locations, in excess of a hundred billion lattice sites in some cases. That means we can accurately resolve the physics at a refined scale for systems that are sufficiently large to satisfy our desire to evaluate and validate these models.
"Summit provides a unique resource that enables us to perform these highly resolved microscale simulations to evaluate and validate this exciting new class of models," he added.
Mark Berrill of the OLCF's Scientific Computing Group collaborated with the team to enable analysis of the high-resolution microscale simulations.
To continue the work, Miller and his team have been awarded another 340,000 node hours on Summit through the 2020 INCITE program.
"While we have the theory worked out for how we can model these systems at a larger scale, we are working through INCITE to evaluate and validate that theory and ultimately reduce it to a routine practice that benefits society," Miller said.
Provided by Oak Ridge National Laboratory