How a seasonal snarl-up in the mid-1500s gave us our strange rules for leap years

Happy February 29! It doesn't come round very often, so make sure you enjoy it.
But why do we have these extra days? Well, if we didn't, the seasons would gradually move around the calendar. Rather than midsummer in the southern hemisphere falling around December 21, it would arrive in January, then February, and so on. After a few centuries, the Australian summer would end up be in July!
But what exactly is a year? The simplest answer is the amount of time it takes for Earth to orbit the Sun. At school, we all learn that that is 365 days. Nice and simple, right?
There's just one problem: there are several different definitions of a year.
The sidereal year
The "sidereal year" is the classic classroom definition. It's the time it takes Earth to complete one lap of the Sun and return to exactly the same place in its orbit, judged by the position of the Sun relative to the background stars.
But one sidereal year doesn't take 365 days. Rather, it takes 365.256 days.
Then there's another problem. In addition to spinning on its axis (which gives us day and night), our planet also wobbles. More accurately, Earth's axis "precesses," spinning around once every 26,000 years or so, like a wobbling spinning top.
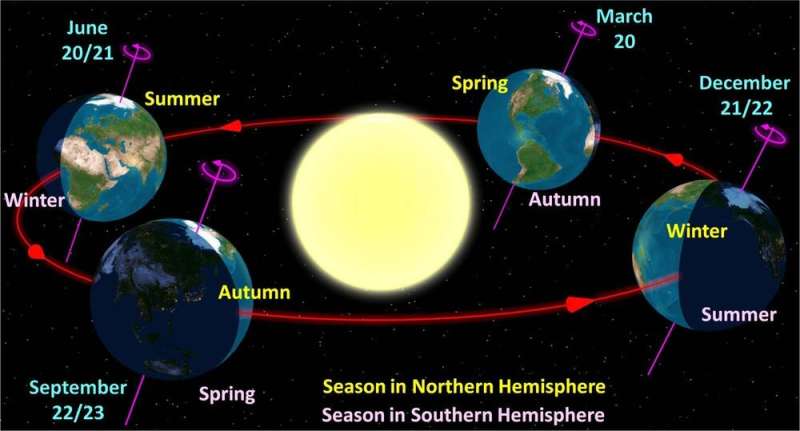
This is important because the direction in which Earth's axis points is what controls the seasons. When the southern hemisphere points away from the Sun, we experience our southern winter while the northern hemisphere sees summer, and then vice versa.
But the precession (wobbling) of Earth's axis means that in 13,000 years' time, the directions would be the opposite of today. Today, the South Pole is angled towards the Sun during the southern midsummer, but in 13,000 years it would be tilted away (midwinter) at the same place in Earth's orbit.
This means that, over thousands of years, the location at which we would experience midwinter or midsummer in Earth's orbit would change. In other words, if we tied our calendar to the sidereal year, the seasons would still shift through the calendar!
The tropical year
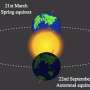
Fortunately, we have another way to define a year that can fix this problem. Instead of measuring the exact time it takes to orbit the Sun, we can instead measure the time between the vernal equinox of one year and the next.
The vernal equinox is the point in Earth's orbit where the Sun moves from the southern hemisphere of our sky to the northern one. Each year it falls on or around March 21.
The time between one equinox and the next is called the "tropical year," and is slightly shorter than the sidereal year. It comes in at 365.24219 days.
This difference is pretty small (about 20 minutes), but it equates to the amount that Earth's axis has precessed in that time—just under 1/26,000 of a full lap.
Leaping into the future
But what does all this have to do with leap years? Well, because the tropical year is not exactly 365 days long, the date of the vernal equinox (and midsummer, midwinter, and any other seasonal event you care to name) will gradually drift through the calendar. If every year had 365 days, those events would gradually fall later and later in the calendar—by 0.24219 days per year.
That doesn't sound like much, but it would mount up. After 100 years, the dates of those events would be 24 days later. The calendar would fall out of alignment with the seasons.
To remedy this, we have leap years, in which we add a single day to the length of the year. If we take a single four-year period, and work out the average length of the year, we get 365.25 days, which is pretty close to the real thing. But it still isn't close enough.
The Julian calendar
This approximation worked well enough for a long time. In 45BC, the predecessor to the modern calendar began. Known as the Julian calendar, it was introduced by Julius Caesar.
The Julian calendar implemented a process of leap years: every fourth year, without fail, there would be an extra day at the end of February.
There were some problems implementing this new calendar—and for a few decades, leap years were incorrectly added every three years. Things were sorted out by 12AD, and from then on, every fourth year had a leap year.
But by the mid-1500s, errors were again beginning to mount. Remember that this approach gives an average year length of 365.25 days, whereas the true tropical year is 365.24219 days.
After one and a half millennia, this small difference had resulted in the dates for the solstices drifting by ten days through the calendar.
The Gregorian calendar
To fix this very slow drift, a new calendar was devised in the second half of the 16th century. Named after Pope Gregory XIII, the Gregorian calendar was released in 1582.

It shifted the dates of the year, moving the solstices back to their intended place. It then tweaked the way leap years were handled, to ensure those dates didn't drift again in the future.
The small change was that leap years that were '"century years" (years ending in 00) had to be divisible by both 100 and 400. If the year can be divided by 100, but not by 400, it's not a leap year.
Let's take the century years 1900 and 2000 as examples. 1900 is divisible by 100, but not by 400. So 1900 wasn't a leap year.
By contrast, 2000 can be divided by both 100 and 400, so it remained a leap year, and is called a "century leap year."
So at the end of the 19th century, the sequence of leap years went: 1892, 1896, 1904, 1908. But at the end of the 20th century, leap years continued without a break (1992, 1996, 2000, 2004).
What does this mean? In the old Julian calendar, there were 100 leap years in every 400 years. But in the Gregorian calendar, we have just 97 for every 400 years.
This gives a remarkably good fit to the length of the tropical year. The average length of one year in the 400-year Gregorian cycle is 365.2425 days. That is almost (but not quite) exactly one tropical year—in fact, the two differ by just 26.8 seconds.
That's close enough that we don't have to worry about our seasons shifting in the calendar for thousands of years to come.
Provided by The Conversation
This article is republished from The Conversation under a Creative Commons license. Read the original article.![]()