New method for calculating optimal trajectories for flight to the moon
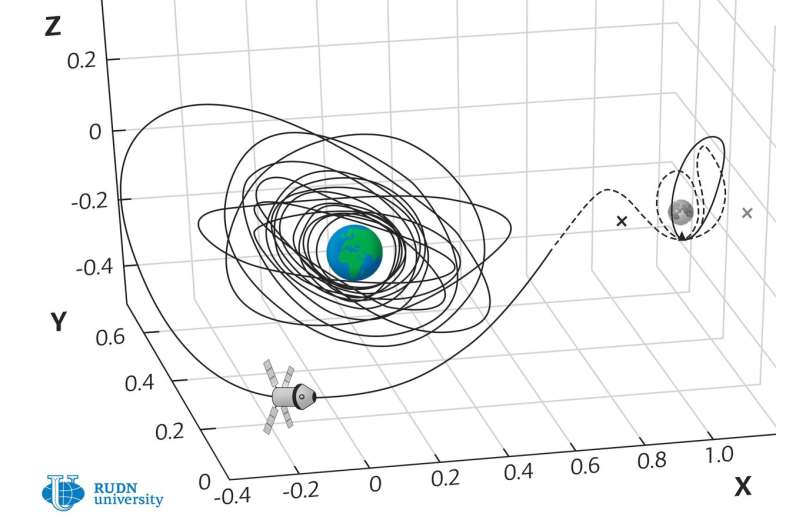
A RUDN University mathematician has developed a method for finding low-cost quasi-optimal trajectories of flight from Earth orbit to the moon for spacecraft with an electric propulsion engine. The trajectories calculated using this method reduce the fuel costs by 56% with a some increase in the flight time. The paper is published in the journal Cosmic Research.
In theoretical future space programs, the moon plays the role of a training base and a transit point for flights to planets, primarily to Mars. Many countries are developing their own programs of exploration and development of the moon. In particular, NASA, together with partners, plans to put a space station into lunar space. This will require delivery of a large amount of cargo to the moon, but the mathematical problem of finding economical flight paths from Earth orbit to the moon does not yet have good solutions.
Alexey Ivanyukhin from RUDN University, together with his colleague Viacheslav Petukhov from the Moscow Aviation Institute, developed a method for searching flight paths to the moon for spacecraft with electric propulsion engine (EPS). In such an engine, thrust is created by the flow of inert gas ions accelerated in an electric field, usually xenon. The thrust is low, but, unlike engines on chemical fuel, they can work not for minutes, but for months.
Mathematicians considered one of the types of lunar orbits—the so-called halo orbits around libration points L1 and L2 of the Earth-moon system. These trajectories will be in demand, because this orbit has been chosen for a near-lunar station, and there is already a Chinese spacecraft Quqiao in a halo orbit around the point L2, designed to relay signals from the lunar probe Chang'e-4 on the far side of the moon.
"Solutions to these problems have been proposed since the 1960s of the 20th century. All possible proposals can be divided according to the degree of proximity of the obtained solution to the optimal (best) one and the use of special effects of the interaction of the Earth and the moon. The first aspect in these problems leads to very complex (almost unsolvable) statements. It takes a lot of time to solve (calculate) and analyze them. Therefore, there is an interest in simplifying the control problem, there can be many of them—our method is based on interpolation of strict optimal solutions obtained in problems close to the one being solved. This allows you to significantly simplify the decision process and implement feedback management. Theoretically, this algorithm can work even on board of a spacecraft autonomously," Alexey Ivanyukhin said.
To solve the problem of three bodies in the Earth-moon system with a low-mass spacecraft, RUDN University mathematician used the feedback control method based on interpolation of a set of optimal controls in typical problems of interorbital flight—quasi-optimal feedback control (QUEUE).
Alexey Ivanyukhin and his colleague used in their research special subset of solutions to the three body problem called sustainable diversity. The trajectories of this variety near the moon are arranged in such a way that the spacecraft inevitably falls into one of the libration points or halo orbits near them. It is possible to reduce flight time and fuel weight due to the gravitational pull of the moon by sending a spacecraft into one of these asymptotic trajectory.
The RUDN University mathematician conducted a numerical experiment for a spacecraft with a final mass of 1000 kilograms and an electric propulsion engine SPD-140D, which is produced by the Fakel experimental design bureau in Kaliningrad. In the experiment, the spacecraft will be launched near Earth's orbit and should reach one of the halo orbits near the moon by April 12, 2026. In the first stage, the spacecraft moves from the initial orbit to one of the asymptotic trajectories near the moon using an electrojet engine. Then the engine shuts off and the spacecraft enters halo orbit under the gravity force.
The trajectories obtained in the calculations showed an advantage over the so-called straight trajectories—that do not use nonlinear effects of the gravitational interaction of the Earth and the moon. During the flight to point L1, the fuel mass can be reduced by 11% while increasing the time in flight by 8-27%. Calculations for destination L2 give trajectories with a 2.4% increase in travel time and a 7% decrease in fuel mass.
"Such flights can be used for lunar automatic vehicles. Unfortunately, they are not suitable for sending a person to the moon or to a station in the vicinity of libration points, since they require too much time. But they can be used to deliver weight. And it is possible that the lunar transport vehicle (similar to the Progress ship) will have an electric propulsion engine and will fly along such trajectories"—a RUDN University mathematician said. He added that the developed method can be used for interorbital flights near the Earth and the moon, but it is not suitable for flights to other planets.
More information: A. V. Ivanyukhin et al. Low-Energy Sub-Optimal Low-Thrust Trajectories to Libration Points and Halo-Orbits, Cosmic Research (2019). DOI: 10.1134/s0010952519050022
Provided by RUDN University




















