Nearly extreme black holes which attempt to regrow hair become bald again

Black holes 'have no hair': no attributes that can be used to tell them apart. Extreme black holes (spinning at maximally allowed rate) can have an additional property, permanent hair that is made of a massless scalar field. Nearly extreme black holes (like Gargantua, the black hole featured in the movie "Interstellar") have hair that is a transient phenomenon: nearly extreme black holes that attempt to regrow hair will lose it and become bald again.
The black holes of Einstein's theory of relativity can be completely described by just three parameters: their mass, spin angular momentum, and electric charge. Since two black holes that share these parameters cannot be distinguished, regardless of how they were made, black holes are said to "have no hair"—they have no additional attributes that can be used to tell them apart.
In the early 1970s the late Jacob Bekenstein provided a proof for the nonexistence of hair made of scalar fields given a set of assumptions on the properties of the latter. Researcher Lior Burko of Theiss Research said, "Since Bekenstein's proof, several papers have found examples for scalar hair, and all these examples violate one or another of the assumptions made by Bekenstein. But in all cases, the hair was made of the scalar field itself."
Recently, it was shown that black holes that are charged by the maximum possible electric charge ("extreme black holes") can have an additional property, permanent hair that is made of a massless scalar field, and that this newly found hair can be observed from a great distance. "A massless scalar hair does not violate any of the assumptions underlying Bekenstein's proof. It was a big surprise for me when this new hair was found by Angelopoulos, Aretakis, and Gajic, so I wanted to look at it in greater detail. It is hair in a different sense than the kinds of hair that were found before. It is not the scalar field itself, but a certain integral on a derivative of the scalar field that is to be calculated on the surface of the black hole, on its event horizon," said Burko.
The new hair can be observed at a great distance, by calculating a different quantity there. "The measurement at a great distance that Angelopoulos, Aretakis, and Gajic found is strictly speaking precise only at infinitely late time," added Burko. "These would be observers who are very distant from the black hole, and who make the measurements in the infinite future. We wanted to see what happens at late but finite times, to see the time dependence of the measurement and how it approaches its asymptotic value. Another special thing about this new hair is that it applies only for exactly extreme black holes, and we wanted to understand what happens when the black hole is nearly extreme, but not exactly extreme."
Burko and his colleagues Gaurav Khanna of the University of Massachusetts Dartmouth and his former student Subir Sabharwal, currently with the Eastamore Group, showed in a paper just published in Physical Review Research that measurements from a great distance are approaching the hair value, with the difference between them decaying with inverse time. But then they went beyond the original model used by Angelopoulos, Aretakis, and Gajic, and generalized the hair to black holes that rotate at the maximum possible spin rate or just close to it.
"In addition to a maximal value of charge, there is also a limit for how fast a black hole can spin. Black holes that spin at the maximal allowed rate are therefore also called extreme black holes. We describe both maximally charged and maximally spinning black holes by the name extreme black holes, as there are many similarities between the two. The new hair was originally found for a very useful toy model for black holes, specifically black holes that are spherically symmetric and electrically charged. But black holes in reality are neither. Instead, we wanted to find out if this hair can be found also for spinning black holes," said Burko. "In the movie 'Interstellar' the monster black hole is nearly extreme. We wanted to see if Gargantua has hair."
The team used very intensive numerical simulations to generate their results. The simulations involved using dozens of the highest-end Nvidia graphics-processing-units (GPUs) with over 5,000 cores each, in parallel. "Each of these GPUs can perform as many as 7 trillion calculations per second; however, even with such computational capacity the simulations took many weeks to complete" said Khanna.
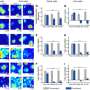
The team showed that for the nearly extreme spinning black holes the hair is a transient behavior. At intermediate times nearly extreme black holes behave like extreme black holes would, but at late times they behave like regular, non-extreme black holes. "Nearly extreme black holes can pretend that they are extreme for only so long. But eventually their non-extremality becomes manifest," Burko summarized. "Nearly extreme black holes that attempt to regrow hair will lose it and become bald again." The team also discusses the observational features, e.g., with gravitational wave observatories such as LIGO/VIRGO or LISA, of the smoking-gun detection of nearly extreme black holes.
More information: Lior M. Burko et al, Transient scalar hair for nearly extreme black holes, Physical Review Research (2019). DOI: 10.1103/PhysRevResearch.1.033106
Provided by Theiss Research