Researchers model avalanches in two dimensions
There's a structural avalanche waiting inside that box of Rice Krispies on the supermarket shelf. Cornell researchers are now closer to understanding how those structures behave—and in some cases, behave unusually.
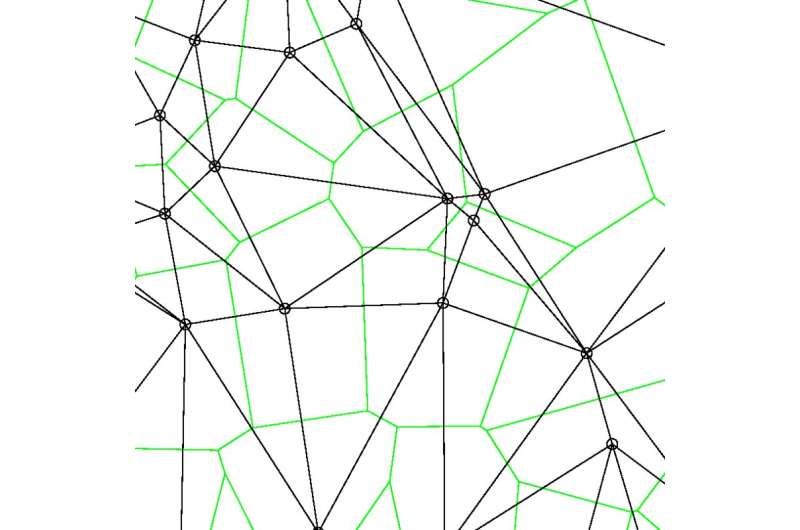
The researchers, led by James Sethna, professor of physics in the College of Arts and Sciences, have for the first time rendered a model for crackling noise in two dimensions. Their paper, "Unusual Scaling for Two-Dimensional Avalanches: Curing the Faceting and Scaling in the Lower Critical Dimension," was published Oct. 30 in Physical Review Research. The paper's lead author was Lorien X. Hayden, M.S. '15, Ph.D. '19, and co-author was Archishman Raju, M.S. '16, Ph.D. '18.
Milk enters Rice Krispies through a process known as "fluid invasion," which is similar to the oil industry's method of pumping pressurized water into porous sandstone to push out oil. The resulting noise—the cereal's famous "snap, crackle and pop"—is a type of tiny "avalanche" that indicates a burst of milk invading pores in the puffed rice. Each avalanche is essentially composed of smaller-scale versions of itself, a proportionality shaped by "power law" distribution. Crackling noise also describes earthquakes, magnets and many other systems.
"We know how to deal with power law scaling," said Sethna, the paper's senior author, "but we've recognized that there are lots of interesting physics problems where that power law scaling doesn't work. But it still looks fractal in the sense that when you magnify things, you see something that looks the same."
Researchers have previously modeled crackling noise in three, four and five dimensions through a process called Widom scaling—a way of accounting for critical-point anomalies that was developed by Benjamin Widom, professor emeritus of chemistry and chemical biology. The critical point is the moment that a system or form of matter transitions into a new phase.
These moments are often marked by unusual behavior, where power laws don't seem to apply.
"I've spent 20 years being puzzled as to how to analyze this very simple model in two dimensions," Sethna said. "I can simulate it, but I couldn't do the Widom scaling. I couldn't figure out the things that replaced the power law. And it irritated me. So I started looking at other problems, 50-year-old problems, and nobody had done them, either."
Sethna's solution was to turn to the work of another groundbreaking Cornellian, the late physicist Kenneth G. Wilson, whose work on quantum fields with a mathematical scheme called the renormalization group expanded on Widom's research and won Wilson the Nobel Prize in physics in 1982.
"Ken Wilson was interested in understanding the behavior of materials as they went through critical points, as they change their behavior in a qualitative way," Sethna said. "We figured out how to do Widom scaling for systems that Widom's method doesn't work for, by using a fancier analysis of the predictions of Ken Wilson's renormalization group."
By tying together several strands of Cornell-grown math methods, the researchers solved a decades-old problem with a new theoretical approach and simulation methods, making an important step toward a fuller understanding of how avalanches and crackling noise behave near critical points.
Rice Krispies may never look, or sound, the same again.
"We've been crippled, I think, by the fact that we didn't really understand, for many cases, the exact nature of how the transitions are happening," Sethna said. "And for the first time, we've really sorted it out. At least much of it."
More information: L. X. Hayden et al. Unusual scaling for two-dimensional avalanches: Curing the faceting and scaling in the lower critical dimension, Physical Review Research (2019). DOI: 10.1103/PhysRevResearch.1.033060
Provided by Cornell University