'Poor man's qubit' can solve quantum problems without going quantum
It may still be decades before quantum computers are ready to solve problems that today's classical computers aren't fast or efficient enough to solve, but the emerging "probabilistic computer" could bridge the gap between classical and quantum computing.
Engineers at Purdue University and Tohoku University in Japan have built the first hardware to demonstrate how the fundamental units of what would be a probabilistic computer—called p-bits—are capable of performing a calculation that quantum computers would usually be called upon to perform.
The study, published in Nature on Wednesday (Sept. 18), introduces a device that serves as a basis for building probabilistic computers to more efficiently solve problems in areas such as drug research, encryption and cybersecurity, financial services, data analysis and supply chain logistics.
Today's computers store and use information in the form of zeroes and ones called bits. Quantum computers use qubits that can be both zero and one at the same time. In 2017, a Purdue research group led by Supriyo Datta, the university's Thomas Duncan Distinguished Professor of Electrical and Computer Engineering, proposed the idea of a probabilistic computer using p-bits that can be either zero or one at any given time and fluctuate rapidly between the two.
"There is a useful subset of problems solvable with qubits that can also be solved with p-bits. You might say that a p-bit is a 'poor man's qubit,'" Datta said.
Whereas qubits need really cold temperatures to operate, p-bits work at room temperature like today's electronics, so existing hardware could be adapted to build a probabilistic computer, the researchers say.
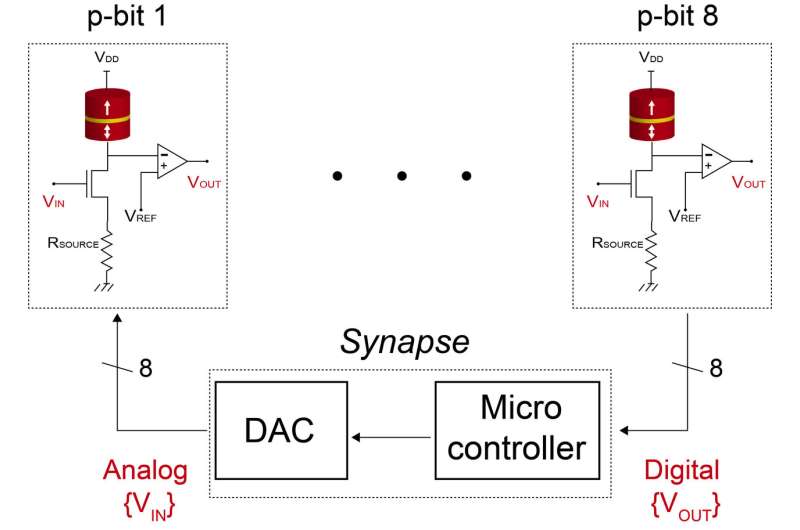
The team built a device that is a modified version of magnetoresistive random-access memory, or MRAM, which some types of computers use today to store information. The technology uses the orientation of magnets to create states of resistance corresponding to zero or one.
Tohoku University researchers William Borders, Shusuke Fukami and Hideo Ohno altered an MRAM device, making it intentionally unstable to better facilitate the ability of p-bits to fluctuate. Purdue researchers combined this device with a transistor to build a three-terminal unit whose fluctuations could be controlled. Eight such p-bit units were interconnected to build a probabilistic computer.
The circuit successfully solved what is often considered a "quantum" problem: Breaking down, or factoring, numbers such as 35,161 and 945 into smaller numbers, a calculation known as integer factorization. These calculations are well within the capabilities of today's classical computers, but the researchers believe that the probabilistic approach demonstrated in this paper would take up much less space and energy.
"On a chip, this circuit would take up the same area as a transistor, but perform a function that would have taken thousands of transistors to perform. It also operates in a manner that could speed up calculation through the parallel operation of a large number of p-bits," said Ahmed Zeeshan Pervaiz, a Ph.D. student in electrical and computer engineering at Purdue.
Realistically, hundreds of p-bits would be needed to solve bigger problems—but that's not too far off, the researchers say.
"In the near future, p-bits could better help a machine to learn like a human does or optimize a route for goods to travel to market," said Kerem Camsari, a Purdue postdoctoral associate in electrical and computer engineering.
More information: Integer factorization using stochastic magnetic tunnel junctions, Nature (2019). DOI: 10.1038/s41586-019-1557-9 , nature.com/articles/s41586-019-1557-9
Journal information: Nature
Provided by Purdue University