Scientists simulate a black hole in a water tank

Certain phenomena that occur in black holes but cannot be directly observed in astronomic investigations can be studied by means of a laboratory simulation. This is possible due to a peculiar analogy between processes that are characteristic of black holes and hydrodynamic processes. The common denominator is the similarity of wave propagation in both cases.
This possibility is explored in a new article published in Physical Review Letters. Physicist Maurício Richartz, a professor at the Federal University of the ABC (UFABC) in Brazil, is one of the authors of the article, produced by Silke Weinfurtner's group at the University of Nottingham's School of Mathematical Sciences in the UK. The research was supported by FAPESP via the Thematic Project "Physics and geometry of spacetime," for which Alberto Vazquez Saa is the principal investigator.
"While this study is entirely theoretical, we've also performed experimental simulations at Weinfurtner's lab," Richartz told Agência FAPESP. "The apparatus consists basically of a large water tank measuring 3 meters by 1.5 meter. The water flows out through a central drain and is pumped back in, so that the system reaches a point of equilibrium in which the quantity of inflow is equal to the quantity of outflow. We simulate a black hole in this way."
He provided further details to explain how this was done. "The water flow speeds up as it approaches the drain. When we produce waves on the surface of the water, we obtain two important velocities: the velocity of wave propagation and the velocity of the overall water flow," he said.
"Far from the drain, wave velocity is much higher than fluid velocity, so waves can propagate in any direction. The situation is different near the drain, however. Fluid velocity is much higher than wave velocity, so the waves are dragged down by the water flow even when they're propagating in the opposite direction. This is how a black hole can be simulated in the lab."
In a real astrophysical black hole, its gravitational attraction captures matter and prevents waves of any kind from escaping, including light waves. In the hydrodynamic simulacrum, the waves on the surface of the fluid cannot escape from the vortex that forms.
In 1981, Canadian physicist William Unruh discovered that the similarity between the two processes – a black hole and a hydrodynamic simulacrum – was more than a mere analogy. With a few simplifications, the equations that describe the propagation of a wave in the vicinity of a black hole are identical to those that describe the propagation of a wave in water flowing down a drain.
This legitimizes the use of hydrodynamic processes to investigate the phenomena typical of black holes. In the new study, Richartz and collaborators analyzed the relaxation (ringdown) process in a hydrodynamic simulacrum of an out-of-equilibrium black hole, taking previously ignored factors into account. In some respects, the phenomenon they studied is similar to the ringdown process in an actual astrophysical black hole that generates gravitational waves after being created by a collision with two other black holes.
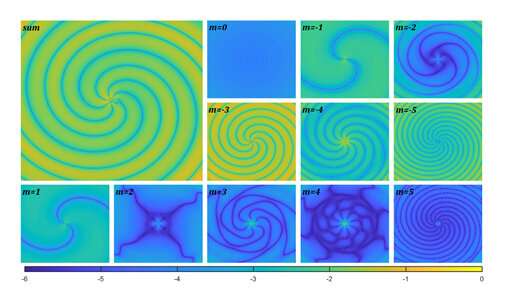
"A careful analysis of the ringdown spectrum reveals the properties of the black hole, such as its angular momentum and mass. In more complex gravitational systems, the spectrum might depend on more parameters […]", the authors write in the article published in Physical Review Letters.
Vorticity
Vorticity is overlooked by the simplest models but is considered in this study. It is a key concept in fluid mechanics that quantifies the rotation of specific regions of a moving fluid.
If the vorticity is null, the region simply accompanies the motion of the fluid. However, if the vorticity is not null, in addition to accompanying the flow, it also spins around its own center of mass.
"In the simpler models, it's generally assumed that the vorticity of the fluid is equal to zero. This is a good approximation for regions of the fluid located at a distance from the vortex. For regions near the drain, however, it isn't such a good approximation because in this case vorticity becomes increasingly important. So one of the things we did in our study was incorporate vorticity," Richartz said.
The researchers set out to understand how vorticity influences wave damping during propagation. When a real black hole is disturbed, it generates gravitational waves that oscillate at a certain frequency. Their amplitude decreases exponentially over time. The set of damped resonances that describes how the excited system is driven back to equilibrium is characterized technically by a spectrum of quasi-normal modes of oscillation.
"In our study, we investigated how vorticity influenced quasi-normal modes in the hydrodynamic black hole analogue. Our main finding was that some oscillations decayed very slowly, or in other words remained active for a long time, and were located spatially in the vicinity of the drain. These oscillations were no longer quasi-normal modes, but a different pattern known as quasi-bound states," Richartz said.
A future development of the research will entail producing these quasi-bound states experimentally in the laboratory.
More information: Sam Patrick et al. Black Hole Quasibound States from a Draining Bathtub Vortex Flow, Physical Review Letters (2018). DOI: 10.1103/PhysRevLett.121.061101
Black hole quasibound states from a draining bathtub vortex flow arxiv.org/pdf/1801.08473v2.pdf.
Journal information: Physical Review Letters
Provided by FAPESP




















