Mathematical monotsukuri: Summing a constant may help to detect synchronized brain activity
Scientists at Tokyo Institute of Technology found a simple, yet effective way to improve how synchronization is measured in chaotic systems. The technique consists of adding a constant parameter to the "analytic signals" in a way that emphasizes certain aspects of their timing. This could improve brain-computer interfaces designed to aid disabled people.
Humans are good at detecting whether separate things happen simultaneously, for example, if two lights flash together or not. When two swings move with a regular motion, it is easy to tell whether there is any temporal relationship or "synchronization." However, the trajectory of some objects, such as kites, can be very complicated while still exhibiting some pattern, even though it may be difficult to detect; such systems are called "chaotic." In physics, chaos does not mean lack of order; it indicates the presence of a very complicated type of order. Chaotic order can be found across many systems, including the activity of neurons.
When trajectories, which do not necessarily correspond to physical movement and can instead represent electrical signals, are sufficiently complicated, it becomes challenging to determine if they are synchronized. In many cases, only some aspects of their motion might be interrelated. Hence, measuring synchronization is difficult and has been the subject of research for decades.
Usually, when a trajectory approximately repeats itself in a loop, it is useful to consider at what point of this cycle the system we are observing is at a given time; we call this its "phase." Meanwhile, when a trajectory is irregular, the size of the loop also changes and each cycle may be larger or smaller than the previous one; this is called the "amplitude." These two aspects are independent and can be extracted from any signal via a mathematical trick called the "analytic signal."
Measuring whether the phases of two systems are related ("phase locked") is crucial across many fields of interest. Obtaining the degree of phase locking between all possible electrode combinations represents a good way of guessing what someone is thinking about via voltages measured via electroencephalogram. Such techniques are not yet very detailed, but can detect some forms of imaginary movements as a data source for brain interfaces to aid disabled people.
However, these brain-computer interfaces are generally slow and inaccurate. Now, researchers in Japan, Poland and Italy propose a new approach to measuring the synchronization between electroencephalogram signals. This research was the result of a collaboration between scientists from Tokyo Institute of Technology, in part funded by the World Research Hub Initiative, the Polish Academy of Sciences in Krakow, Poland, and the University of Catania, Italy.
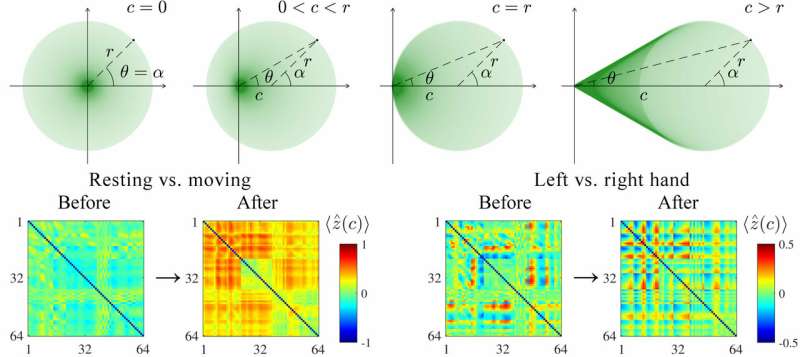
The idea is straightforward and consists of adding a constant after calculating the "analytic signal"; this effectively has a warping effect, as shown in Figure 1. One consequence is that synchronization between the phases and amplitudes of two signals is captured jointly in a way that depends on the value of this added constant.
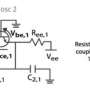
The research team first analyzed the effects of adding this constant in simple theoretical systems before moving on to more representative cases, such as a network of transistor oscillators. Then they applied their approach to a dataset of electroencephalogram signals for which users were told either to rest or imagine moving their left or right hand. The added constant clearly helped the team measure the synchronization between electrodes, ultimately allowing them to increase the classification accuracy for these imaginary actions.
Although simple, the approach resulted in significant improvements in the cases analyzed by the team. In future efforts, they will continue to investigate this method so that it hopefully has an impact in practical applications.
More information: Ludovico Minati et al, Warped phase coherence: An empirical synchronization measure combining phase and amplitude information, Chaos: An Interdisciplinary Journal of Nonlinear Science (2019). DOI: 10.1063/1.5082749
Provided by Tokyo Institute of Technology