A novel solver for approximate marginal map inference
There is a deep connection between planning and inference, and over the last decade, multiple researchers have introduced explicit reductions showing how stochastic planning can be solved using probabilistic inference with applications in robotics, scheduling, and environmental problems. However, heuristic methods and search are still the best-performing approaches for planning in large combinatorial state and action spaces. My co-authors and I take a new approach in our paper, "From Stochastic Planning to Marginal MAP" (authors: Hao Cui, Radu Marinescu, Roni Khardon), at the 2018 Conference on Neural Information Processing Systems (NeurIPS) by showing how ideas from planning can be used for inference.
We developed the Algebraic Gradient-based Solver (AGS), a novel solver for approximate marginal MAP inference. The algorithm builds an approximate algebraic computation graph capturing marginals of state and reward variables under independence assumptions. It then uses automatic differentiation and gradient-based search to optimize action choice. Our analysis shows that the value computed by AGS computation graph is identical to the solution of Belief Propagation (BP) when conditioned on actions. This provides an explicit connection between heuristic planning algorithms and approximate inference.
More specifically, we revisit the connection between stochastic planning and probabilistic inference. We propose for the first time to use an efficient heuristic algorithm which was designed originally for solving planning problems to tackle a central inference task for probabilistic graphical models, namely the marginal maximum a posteriori probability (MMAP) task.
Probabilistic graphical models such as Bayesian networks or Markov networks provide a very powerful framework for reasoning about conditional dependency structures over many variables. For such models, the MMAP inference query is a particularly difficult yet important task, corresponding to finding the most probable configuration (or maximizing the probability) over a subset of variables, called MAP variables, after marginalizing (or summing over) the remainder of the model.
MMAP inference arises in many situations, especially in diagnosis and planning tasks, in which the most natural specification of the model contains many variables whose values we do not care about predicting, but which create interdependence among the variables of interest. For example, in a model-based diagnosis task, given observations, we seek to optimize over a subset of diagnosis variables representing potentially failing components in a system.
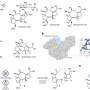
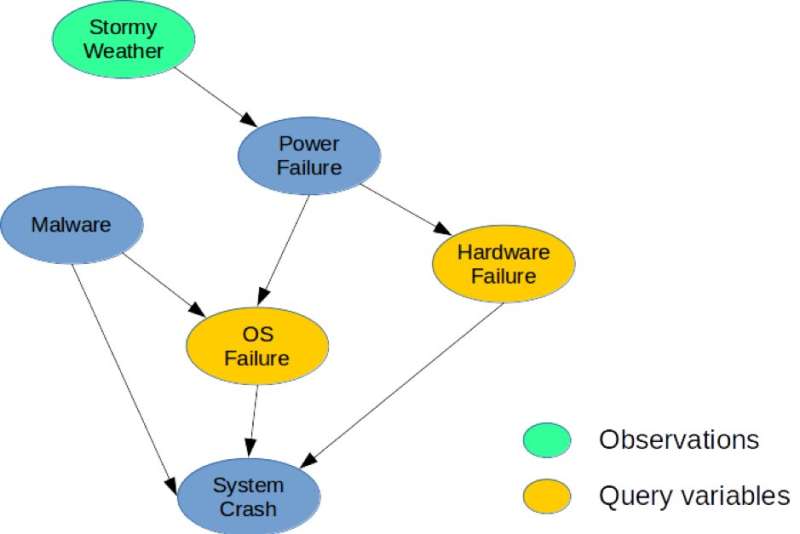
For illustration, consider the Bayesian network shown in Figure 1, which depicts a simple diagnosis problem for a computing system. The model captures direct causal dependencies between six random variables used to describe this problem. Specifically, a System Crash may be caused by a Hardware Failure, an OS Failure, or the presence of Malware in the system. Similarly, a Power Failure could be common cause for Hardware and OS Failure, and Stormy Weather may cause the Power Failure. A possible MMAP query would be to compute the most likely configuration of Hardware and OS Failures, given that we observe Stormy Weather, regardless of the state of the other variables (Malware, System Crash, or Power Failure).
Stochastic planning frameworks such as Markov decision processes are widely used to model and solve planning tasks under conditions of uncertainty. Finite horizon planning can be captured using a dynamic Bayesian network (DBN) where state and action variables at each time step are represented explicitly and the conditional probability distributions of variables are given by the transition probabilities. In off-line planning, the task is to compute a policy that optimizes the long-term reward. In contrast, in on-line planning we are given a fixed limited time t per step and cannot compute a policy in advance. Instead, given the current state, the algorithm must decide on the next action within time t. Then the action is performed, a transition and reward are observed and the algorithm is presented with the next state. This process repeats and the long-term performance of the algorithm is evaluated.
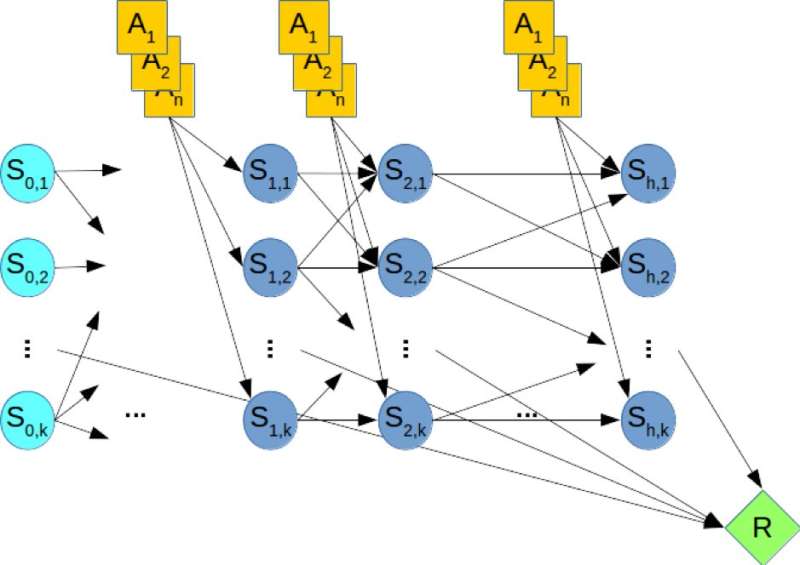
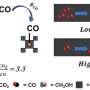
For illustration, consider Figure 2, which shows the DBN corresponding to a hypothetical planning problem, where the orange nodes represent the action variables, the blue nodes denote the state variables, and the green node denotes the cumulative reward that must be maximized. Therefore, computing the optimal policy of the planning problem is equivalent to solving a MMAP query over the DBN, where we maximize over the action variables and marginalize out the state variables.
Our experimental evaluation of difficult MMAP problem instances shows conclusively that the AGS scheme improves over the anytime performance of state-of-the-art algorithms on MMAP problems with hard summation sub-problems, sometimes by up to one order of magnitude. We believe that these connections between planning and inference can be further explored to yield improvements in both fields.
More information: From Stochastic Planning to Marginal MAP: homes.sice.indiana.edu/rkhardo … 018-sogbofa-mmap.pdf
Provided by IBM
This story is republished courtesy of IBM Research. Read the original story here.