It's time for a hyper-crash, say multifractal analyses of the main stock market index

The near future of the global economy looks extremely bleak. This pessimistic forecast comes from advanced statistical analysis of the S&P 500 stock market index, recently published by scientists from the Institute of Nuclear Physics of the Polish Academy of Sciences in Cracow. Based on their analysis, the researchers explain why, in up to a dozen or so years, we can expect an unprecedented financial meltdown.

Black Monday, the bursting of the dot-com bubble and the bankruptcy of the Lehman Brothers shook up the global economy. Soon, however, we may have to deal with such a gigantic collapse of financial markets that all previous crashes will appear as minor stumbling blocks in comparison. This catastrophic vision emerges from the multifractal analysis of financial markets presented in the pages of Complexity by scientists from the Institute of Nuclear Physics of the Polish Academy of Sciences (IFJ PAN) in Cracow—and it coincides with their previous forecasts from a dozen or so years ago.

"The data is, unfortunately, quite unambiguous. It seems that since the mid-2020s, a global financial crash of a previously unprecedented scale is highly probable. This time, the change will be qualitative, indeed radical," says Prof. Stanislaw Drozdz (IFJ PAN, Cracow University of Technology).

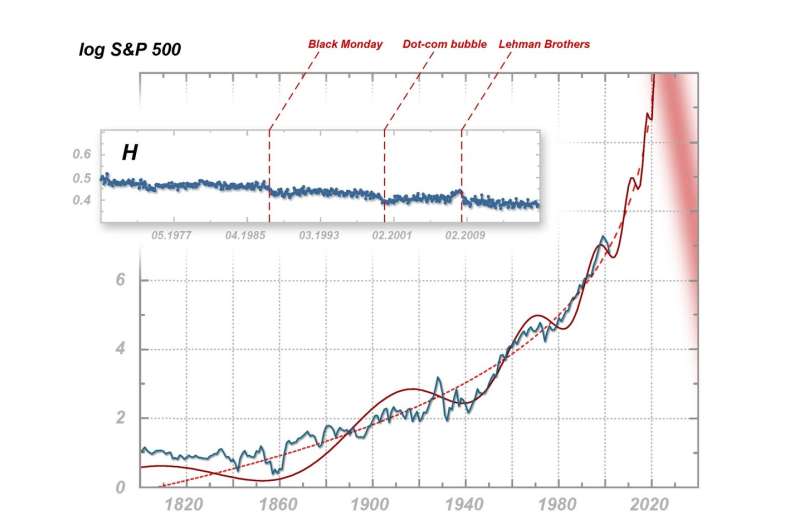
In their latest publication, scientists from the IFJ PAN looked at various economic data, including the daily listing of Standard & Poor's 500 index in the period from January 1950 to December 2016. The main goal of the Cracow researchers' article was not to make catastrophic forecasts, but to credibly present issues related to the occurrence of multifractal effects in the financial time series (i.e. prices or stock market indices). The scientists' attention was especially drawn to a graph showing changes in the Hurst exponent, calculated for the S&P 500 based on multifractal spectra obtained during the analysis.

The Hurst exponent can assume values from 0 to 1 and reflects the degree of susceptibility of a system to a change in trend. A value equal to 0.5 means that in the next measurement, the fluctuating tested value has the same probability of changing up as of changing down. Values below 0.5 indicate a greater tendency to alternation in the directions of fluctuation: a rise in value increases the probability of a decrease or vice versa, which in the context of finances can be interpreted as a symptom of nervousness. Values above 0.5 indicate the persistent nature of the changes and the tendency for the system to build a trend. After an increase, there is then a higher probability of another increase, and after a decrease—a greater subsequent fall.

Stable, mature markets are recognized as being those whose Hurst exponent is equal to 0.5 or shows only slight deviations from this value. The Hurst graph for the S&P 500 does actually start at 0.5. On October 19, 1987, however, there was a crash—Black Monday. The exponent then slightly decreased, but for more than a decade, it remained relatively stable again. At the turn of the century, there was a clear fall, and by March 2000, the dot-com bubble had burst. Just as before, the Hurst exponent again stabilized, but for a shorter period. At the end of the first decade, it suddenly began to grow rapidly, only to fall after the bankruptcy of Lehman Brothers in September 2008. From that moment, the Hurst exponent not only did not return to the value of 0.5, but in the last decade, it has quite clearly and systematically fallen below the particularly worrying value of 0.4.

"What is also striking in the changes in the Hurst exponent for the S&P 500 is the shortening time intervals between consecutive crashes and the fact that after each collapse, the indicator never returns to its original level. We have a clear signal here that the nervousness of the world market is growing all the time, for decades, regardless of changing people, business entities or technology," notes Prof. Drozdz.

This observed dependence corresponds with another detected by Prof. Drozdz and his colleagues already in 2003. In their publication in Physica A: Statistical Mechanics and its Applications, one of the graphs shows the changes of the logarithm from the S&P 500 index starting from 1800 (values from before the introduction of the S&P 500 were reconstructed on the basis of historical data). The zig-zag curve bends along a sinusoid of increasing frequency, ever more dynamically ascending to the asymptote located around 2025. Each subsequent crash is preceded by smaller swings, quasi-mini-crashes, which have been called precursors. Many of the precursors have their own still smaller precursors, thus showing some self-similarity.

"The thing is that analogous self-similar dependence can also work on larger time scales. In which case, all previous crashes would only be precursors of a much larger and more dangerous event. When we come across a process with similar dynamics in physics, we talk about phase transition of the second type, such as the appearance or disappearance of magnetic properties in magnetic material around the Curie temperature," says Prof. Drozdz.

The question concerning the credibility of such a pessimistic forecast remains open. If financial markets do not change qualitatively in the coming years, the worst-case scenario of the development of events has the chance of becoming a reality. However, the significant difference between the worlds of mathematics or physics and the world of finance is key. Mathematical laws and models constructed within physics are effective and relatively uncomplicated, due to the internal simplicity and immutability of the objects they concern. Financial markets are much more complex. Their participants are changeable: They remember, they learn, they can react both logically and emotionally. There is no shortage of examples proving that when knowledge about a law with the power to forecast is disseminated among a significant number of market participants, the market changes rapidly and the detected regularity disappears. Will the same happen in the case of the impending hyper-crash?

The problem is that we do not know what would have to affect the global market to prevent the impending collapse. It is not even certain whether known remedies could be introduced in time—and time is running out, according to the researchers. The future of the world economy from the mid-2020s thus appears very gloomy.

"Probably, we are the only ones who can't lose on this forecast. If the hyper-crash does occur, we will have shown the power of our multifractal statistical tools in a spectacular way. Personally, however, I would prefer for this not to happen. If this is the case and the hyper-crash does not occur, we will still have the quite acceptable interpretation that our forecast was correct, but today's press release will have influenced the behaviour of market participants and, we have just saved the world," notes Prof. Drozdz.