Multifractals suggest the existence of an unknown physical mechanism on the Sun
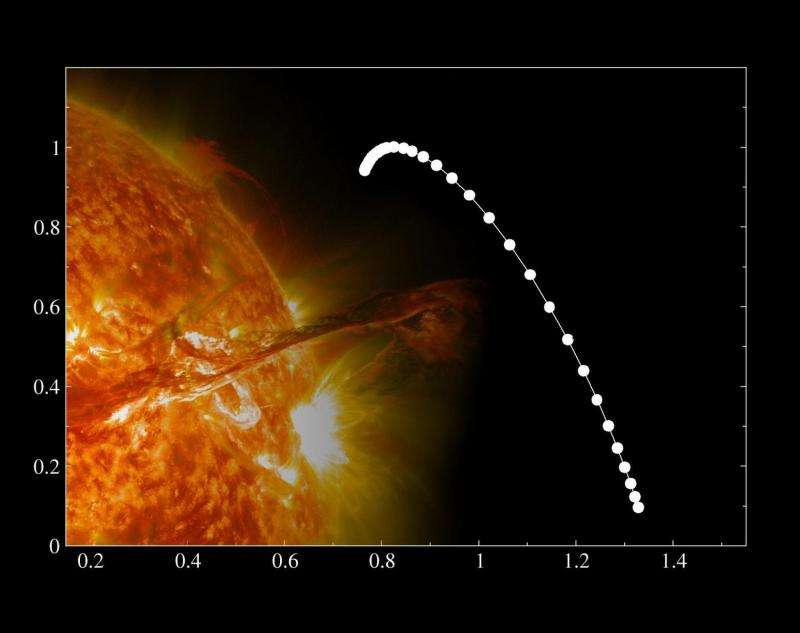
The famous sunspots on the surface of the sun result from the dynamics of strong magnetic fields, and their numbers are an important indicator of the state of activity on the sun. At the Institute of Nuclear Physics of the Polish Academy of Sciences in Kraków, Poland, researchers have been conducting multifractal analysis into the changes in the numbers of sunspots. The resulting graphs were surprisingly asymmetrical in shape, suggesting that sunspots may be involved in hitherto unknown physical processes.
Mathematical analysis of multifractals provides invaluable information on the dynamic phenomena, as they occur to varying degrees of complexity. The results are useful in a number of ways, but most importantly, they allow researchers to discard the influence of current, longstanding trends. In an article published in the journal Physical Review E, scientists at the Institute of Nuclear Physics of the Polish Academy of Sciences (INP PAS) in Krakow, Poland, have shown for the first time that certain overlooked features of the graphs of multifractals, known as singularity spectra of the time series, have a close relationship with the nature of sunspots.
"The graphs generated by the analysis of multifractals reveal a certain asymmetry, and we've turned our attention towards that. Until now, the asymmetry was treated as a byproduct of the computational method. We have proven that the asymmetry might carry valuable information about the nature of the analyzed processes. Using this approach, looking at some of the graphs like those regarding the number of sunspots on the face of the sun, we come to some very interesting conclusions," says Prof. Stanislaw Drozdz (INP PAS, Krakow University of Technology).
Fractals have a characteristic quality of self-similarity: every fragment retains a resemblance to its initial form, even after magnification or reduction. It's notable that the rescaling of any given fragment of an ordinary fractal takes place at the same rate: if we enlarge a fractal x number of times in one place, structures similar to the original appear, and if done in a different location, the enlargement will occur in the same way. Some fractals are so distinctive that they have gained fame even in popular culture. These include, among others, the Sierpinski triangle constructed in 1915 by Waclaw Sierpinski, and the characteristic set described for the first time by the French mathematician of Polish origin, Benoit Mandelbrot. It turns out, however, that there may be more advanced mathematical structures, constructed from fractals 'interwoven' with each other in an certain manner using proper proportions.
"In a sense, multifractals are fractals of fractals. They aren't merely the sum of fractals and they cannot be divided to return to their original components, because the way they 'weave' is fractal in nature. That specific weave causes each fragment of a multifractal to enlarge at a different rate," explains Dr Pawel Oswiecimka (INP PAS), the co-author.

A prototypical multifractal can be constructed at breakfast. All you need is butter and a piece of bread. Divide the slice into halves, but don't cut it. Take some butter and spread it on one half, and spread some more butter on the other half. Then divide each half into halves again and divide each smear, using half of the amount of butter as before but in the same proportions. As the process is repeated any number of times, the distribution of butter on a slice would be multifractal in nature, as the assumed disparity in the amount of butter within each pair of halves becomes more pronounced.
Tests carried out using multifractals disclose the properties encoded in the data relating to the relationships on different scales. The basic graphic tools here are known as multifractal spectra or spectra of singularity.
"If the data take the structure of a simple fractal, the multifractal graphs are reduced to a point. If the structure of a multifractal is homogenous, then the graph takes the ideal symmetrical form, that of a neat hill - an inverted parabola. The thing is, with many graphs we've seen on the actual data, there is no ideal symmetry. As a rule, the left side is dominant," says Dr Oswiecimka.
Left-handed asymmetry shows up in a number of datasets. Upon analyzing the variety of sentence lengths in literary works, most of the graphs which result do not take the structure of a multifractal. The notable exceptions to this are the 'stream of consciousness' novels, best exemplified by James Joyce's "Finnegan's Wake". Under analysis, this and other works of the genre, such as "Rayuela" by Julio Cortazar and "2666" by Roberto Bolaño, turn out to have a structure with pronounced left-handed asymmetry. This means that the relevant correlations show up mainly in the variations between longer sentences, while in the shorter sentences such correlations virtually disappear.
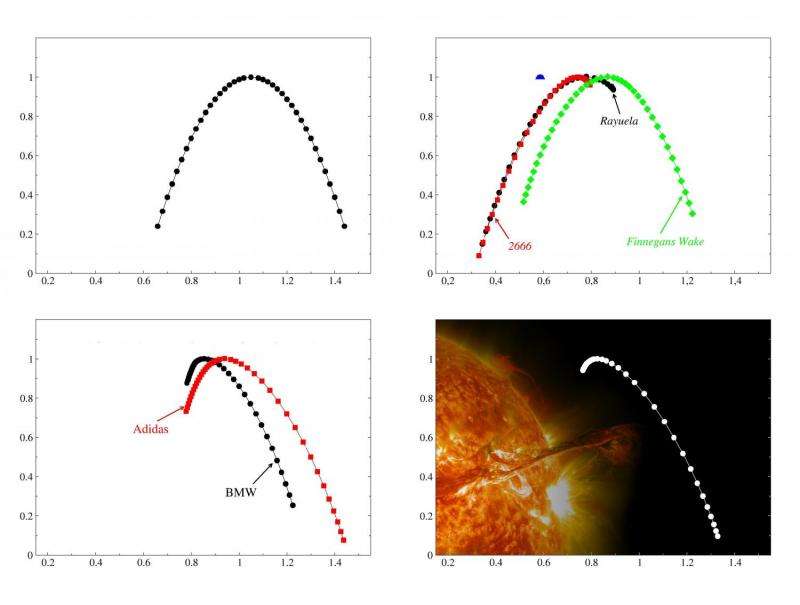
There are, however, phenomena that reveal signs of right-handed asymmetry. Among them is the sequence of time intervals on a stock exchange when there is a change in share prices, which does not happen uniformly. On the contrary, there are long periods when the price in the absence of transactions remains constant, then suddenly in a short time, a cluster of exchanges is registered. Right-handed asymmetry means then, that while the intervals between clusters are poorly correlated, basically random, the inter-transaction times within the clusters are specifically related.
The most curious observation came to light when the INP PAS physicists started to analyze the numbers of sunspots. The surprise was that the graph didn't merely show multifractals, but surprisingly, a pronounced right-handed symmetry. Thus, when the fluctuations in the sunspots have a greater amplitude, its changes are random, and they become more correlated for lower amplitude fluctuations.
"Right-handed asymmetry in the case of the intervals between transactions in the stock market, that we can understand. Nothing happens for some time, somebody suddenly buys or sells, and then others join the trading activity. But what mechanism is responsible for the multifractal correlations in fluctuations of the number of sunspots, and particularly for their dual nature?" wonders Prof. Drozdz.
The results of multifractal analysis in changes to sunspots seem to support the hypothesis that the sun may function with not one but two mechanisms responsible for the generation of magnetic fields. The research will continue in cooperation with the Belgian Royal Observatory in Brussels.
More information: "Detecting and interpreting distortions in hierarchical organization of complex time series"; S. Drożdż, P. Oświęcimka; Physical Review E 91, 030902(R) (2015); DOI: 10.1103/PhysRevE.91.030902
Journal information: Physical Review E
Provided by Polish Academy of Sciences












.gif)





