Mathematicians propose first continuous self-organised criticality model

An international group of researchers (the first author is Nikita Kalinin, Higher School of Economics—Saint-Petersburg, the last author is Ernesto Lupercio, CINVESTAV, Mexico) has presented the first continuous model describing self-organised criticality. The proposed solution is simpler and more universal than the classical sandpile model. It integrates areas as remote from one another as economics, developmental biology, and gravity in the context of tropical geometry. The paper was published in Proceedings of the National Academy of Sciences.

A system is said to be in a critical state if an external force, however small, can produce an avalanche effect causing a change in the system's behaviour. These include phase transitions: Once a single ice crystal emerges in water cooled to zero degrees Celsius, an ice cluster will immediately begin to form.

There are certain dynamical systems that tend toward a critical state—earthquakes are an illustrative example. While a certain temperature and pressure are required for water to freeze, no precise parameters need to be met for an earthquake to happen. The main cause of earthquakes is the continuous movement of tectonic plates, and predicting the exact moment when the system will achieve a critical state and produce an avalanche is virtually impossible.

Many researchers have attempted to solve the mystery of earthquakes. In the mid-20th century, American seismologists Gutenberg and Richter showed a relationship between the magnitude and total number of earthquakes in any given region. This relationship is described by the power law expressed as a straight line on a double logarithmic scale.

Phenomena sharing this characteristic have since been found in geophysics, cosmology, economics, risk management theory and other fields. All of them can be described by the theory of self-organised criticality (SOC).

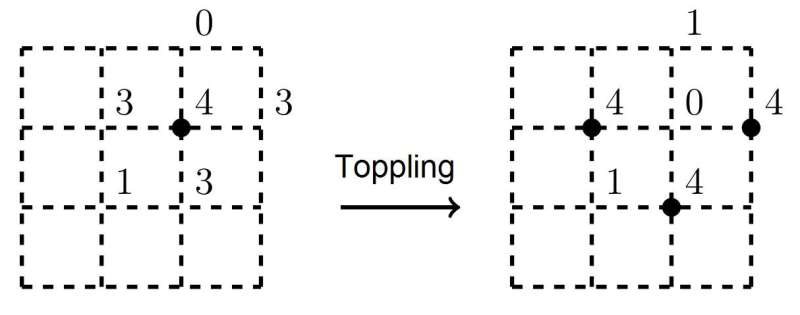
The concept of SOC was introduced by Per Bak, Chao Tang and Kurt Wiesenfeld in 1987. In their seminal paper, they put forward the archetypal example of an SOC system: the Sandpile Model. Imagine a square grid with sand grains in each of its vertices, in which new grains are falling on the grid at a certain frequency. It is assumed that if there are no more than three sand grains in each vertex, the system will remain stable. But as soon as a fourth sand grain falls on top of a vertex, it topples, and the sand slides down this peak and gets redistributed to neighbouring vertices. The toppling will continue in an avalanche until the system returns to equilibrium. The physicists' key discovery was that the number of vertices that topple (i.e. the size of the collapsed region) satisfies a power-law distribution.

The sandpile model has long been the classical model describing SOC. However, it describes the dynamics of critical systems only at the phenomenological level and cannot be used to simulate an earthquake or predict the behaviour of a real sandpile.

"The old sandpile model, being purely combinational, stands somewhat apart from the big world of mathematics. Our model is a step forward, because it has all the advantages of the sandpile model, but it is also geometric and continuous, making it much easier to use," explains author Nikita Kalinin, senior research fellow of the HSE International Laboratory of Game Theory and Decision Making. "We have shown that power law correlations can be obtained in a continuous system that is not a cellular automaton with the help of tropical geometry, which has many applications today."

"Tropical geometry is a twenty-first century branch of geometry inspired by classical algebraic geometry that has flourished because of its connections to many fields of science, primarily string theory," says Dr. Ernesto Lupercio from the CINVESTAV.

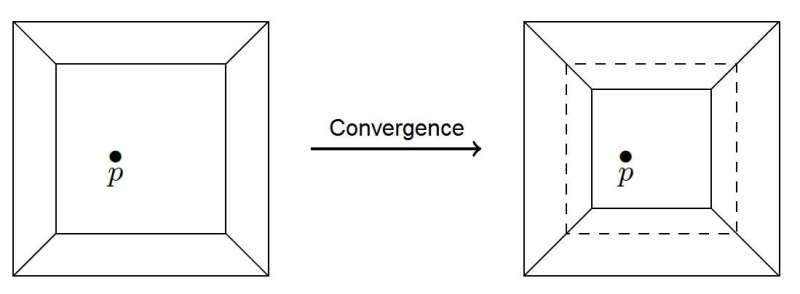
Instead of the grid used in the classical sandpile model, the new tropical sandpile model considers a tropical curve—a planar graph with rectilinear edges—enclosed in a square. The curve divides the square into polygonal regions, each containing a randomly chosen set of points. When a new point is added, the tropical curve tries to pass through it, and the polygonal region containing the point is pulled together via a parallel transfer of its edges. As soon as one of the edges hits the point, the process stops. A new point is then added, and it starts all over again. The previous point may be off the curve again, and the system will start moving towards it.

This convergence process is a finite variant of adding sand grains to a sandpile. In the new model, the avalanche size corresponds to the area swept by the converging regions in the process initiated by adding a random point. The scientists hope that their model will help clarify the relationships between different phenomena manifesting SOC properties.

"We can observe similarities in different phenomena seen through the lens of mathematics. Tropical geometry has applications in string theory, economics and developmental biology. The value of our work lies in finding connections in unexpected places. It means that the methods applied to one area can be applied to another one. You only need to take the next step," says Kalinin.