One fractal quantifies another, mathematicians find

To humor mathematicians, picture a pile of sand grains – say, a billion – in one square of a vast sheet of graph paper. If four or more grains occupy a single square, that square topples by sending one grain to each of its four neighboring squares.
Keep zooming out so the squares become very small, and something strange happens – the sand still "remembers" that it used to live on a square lattice, and a distinctive pattern emerges. Beautiful to boot, this phenomenon, which has stumped mathematicians for decades, is called the Abelian sandpile fractal.
Cornell mathematicians offer a new way of seeing this fractal, by quantifying how its formation depends on that original square grid. This quantification might reveal new insights into the concept of "self-organized criticality," which is when a few simple rules result in complex patterns. It turns out this quantification is another fractal, one more familiar to the math world, called an Apollonian circle packing.
This new quantification is detailed in a paper, submitted for publication, by Lionel Levine and Charlie Smart, both Cornell assistant professors of mathematics, and Wesley Pegden of Carnegie Mellon University.
"We're trying to figure out why this simple rule produces such a complicated fractal," Levine said. Studying such outcomes could apply to many kinds of self-organized systems – for example, the way wildfires spread, or how earthquakes cluster around specific fault lines.
"We can't say exactly when an earthquake will occur," Levine said. "That's because the systems are incredibly complicated. One thing that would help improve predictions would be if we knew what particular details in the fault system to focus on – which are relevant and which are unimportant."
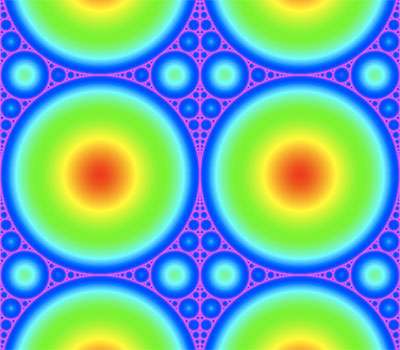
In the sandpile fractal, the detail that might seem unimportant – the fact that it started out on a square grid – actually is crucial, Levine said. And the Apollonian circle packing measures the sandpile fractal's "memory" of that grid.
"No one ever expected that these two fractals would be connected," Smart said. "The fact that they are is spectacular."
Provided by Cornell University












.gif)






