June 22, 2018 report
How community structure affects the resilience of a network
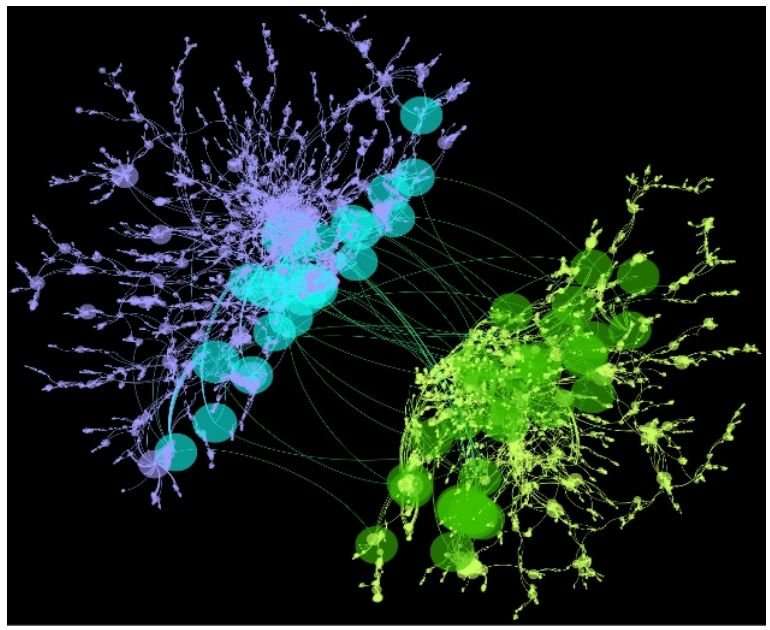
Network theory is a method for analyzing the connections between nodes in a system. One of the most compelling aspects of network theory is that discoveries related to one field, such as cellular biology, can be abstracted to a form that applies directly to a completely different field, like interstate traffic patterns. The most well-known application of network theory is social networking. In a social network, each person is a node connected to other nodes. Additionally, a fraction of nodes within one network, so-called interlinks, will connect to nodes in neighboring networks.
This type of complex, overlapping network is referred to as a community structure. Characterizing these structures is fundamental in the study of networked systems, but researchers haven't fully understood how community structure affects the resilience of the network. An international collaborative of researchers has developed the first theoretical framework demonstrating that community structure significantly affects the resilience of a system; their findings have wide ranging applications in social, technological, biological and climatic systems. They have published their new theoretical framework in the Proceedings of the National Academy of Sciences.
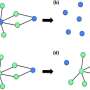
System resilience is a way of describing the robustness of a network. To explore the effects of community structure on resilience, the researchers applied a theory called percolation. Basically, percolation theory seeks the probability of an open path across a network. Percolation is strongly influenced by the number of interlinked nodes within a network.
It is not possible for all nodes in a network to become interlinks. As an example, the authors cite international airports: "Only some airports have the longer runways, customs administration, and passport control required for international flights, and when an airport node already has interconnections, the costs of adding additional interconnections is significantly lower." By contrast, a smaller airport without these infrastructural advantages would not be able to connect to airports in other countries. This is analogous to people who possess the social facility to interlink different network neighborhoods, or brain cells that have the morphological capacity to interlink brain structures.
The researchers found that the interlinks between different communities deeply affect the percolation phase transition—they liken the fraction of nodes with interconnections to an external field in a physical phase transition. They report that systems become more stable and resilient as the fraction of nodes with interconnections increases. In terms of social networks, the greater the number of popular, cross-community people within a network, the more resilient the network will be to external forces like political upheaval or natural disasters.
The authors emphasize that their results apply to other types of networks. They write, "Although our theory is applied here to study the resilience of modules within a single network, it can be extended to study resilience of interdependent networks and multiplex networks."
More information: Resilience of networks with community structure behaves as if under an external field. Proceedings of the National Academy of Sciences doi.org/10.1073/pnas.1801588115
Abstract
Although detecting and characterizing community structure is key in the study of networked systems, we still do not understand how community structure affects systemic resilience and stability. We use percolation theory to develop a framework for studying the resilience of networks with a community structure. We find both analytically and numerically that interlinks (the connections among communities) affect the percolation phase transition in a way similar to an external field in a ferromagnetic– paramagnetic spin system. We also study universality class by defining the analogous critical exponents δ and γ, and we find that their values in various models and in real-world coauthor networks follow the fundamental scaling relations found in physical phase transitions. The methodology and results presented here facilitate the study of network resilience and also provide a way to understand phase transitions under external fields.
Journal information: Proceedings of the National Academy of Sciences
© 2018 Phys.org