New proof reveals fundamental limits of scientific knowledge
A new proof by SFI Professor David Wolpert sends a humbling message to would-be super intelligences: you can't know everything all the time.
The proof starts by mathematically formalizing the way an "inference device," say, a scientist armed with a supercomputer, fabulous experimental equipment, etc., can have knowledge about the state of the universe around them. Whether that scientist's knowledge is acquired by observing their universe, controlling it, predicting what will happen next, or inferring what happened in the past, there's a mathematical structure that restricts that knowledge. The key is that the inference device, their knowledge, and the physical variable that they (may) know something about, are all subsystems of the same universe. That coupling restricts what the device can know. In particular, Wolpert proves that there is always something that the inference device cannot predict, and something that they cannot remember, and something that they cannot observe.
"In some ways this formalism can be viewed as many different extensions of [Donald MacKay's] statement that 'a prediction concerning the narrator's future cannot account for the effect of the narrator's learning that prediction,'" Wolpert explains. "Perhaps the simplest extension is that, when we formalize [inference devices] mathematically, we notice that the same impossibility results that hold for predictions of the future—MacKay's concern—also hold for memories of the past. Time is an arbitrary variable—it plays no role in terms of differing states of the universe."
Not everyone can be right
What happens if we don't require that an inference device know everything about their universe, but only that it knows the most that could be known? Wolpert's mathematical framework shows that no two inference devices who both have free will (appropriately defined) and have maximal knowledge about the universe can co-exist in that universe. There may (or not) be one such "super inference device" in some given universe—but no more than one. Wolpert jokingly refers to this result as "the monotheism theorem," since while it does not forbid there being a deity in our universe, it forbids there being more than one.
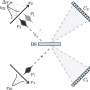
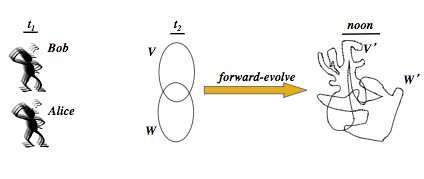
As an example, suppose that Bob and Alice are both scientists with unlimited computational abilities. Moreover, suppose that they both have "free will," in that the question Bob asks himself does not restrict the possible questions Alice could ask herself, and vice-versa. (This turns out to be crucial.) Then it is impossible for Bob to predict (or retrodict) what Alice thinks at another time if Alice is also asked to predict what Bob is not thinking at that time.
Wolpert compares this proposition to the Cretan liar's paradox, in which Epimenides of Knossos, a Cretan, famously stated "all Cretans are liars." Unlike Epimenides' statement though, which exposes the problem of systems that have the capability of self-reference, Wolpert's reasoning also applies to inference devices without that capability.
In addition, in Wolpert's formalism, the same scientist, considered at two different moments in time, is two different inference devices. So while it could be that some inference device is a "super inference device" at one moment, they could not be so more than once. Again tongue in cheek, he refers to this as the "deism" theorem, since it allows there to be a deity that knows the most that could be known at the beginning of the universe—but forbids their ever being so knowledgeable again.
Because it does not rely on specific theories of physical reality like quantum mechanics or relativity, the new proof presents a broad set of limits for exploring the nature of scientific knowledge.
"None of these results limiting knowledge acquired by prediction relies on there being chaotic processes in the universe… it doesn't matter what the laws of physics are or if Alice is more computationally powerful than a Turing machine," says Wolpert. "All of this is independent of that and it's much broader ranging."
This research is progressing in many different directions, ranging from epistemic logic to a theory of Turing machines. In particular, Wolpert and his colleagues are creating a more nuanced, probabilistic framework that will allow them to explore not only the limits of absolutely correct knowledge, but also what happens when the inference devices are not required to know with 100% accuracy.
"What if Epimenides had said 'the probability that a Cretan is a liar is greater than x percent?'" Moving from impossibility to probability could tell us whether knowing one thing with greater certainty inherently limits the ability to know another thing. According to Wolpert, "we are getting some very intriguing results."
More information: Read David Wolpert's "Theories of Knowledge and Theories of Everything" chapter in the The Map and the Territory: www.springer.com/us/book/9783319724775
Constraints on physical reality arising from a formalization of knowledge: arXiv:1711.03499 [physics.hist-ph] arxiv.org/abs/1711.03499
Provided by Santa Fe Institute