New math bridges holography and twistor theory

The modern-day theoretical physicist faces a taxing uphill climb. "As we learn more, reality becomes ever more subtle; the absolute becomes relative, the fixed becomes dynamical, the definite is laden with uncertainty," writes physicist Yasha Neiman.
A professor and head of the Quantum Gravity Unit at the Okinawa Institute of Science and Technology Graduate University (OIST), he grapples with this conundrum on a daily basis. Quantum gravity, Neiman's branch of physics, aims to unify quantum mechanics, which describes nature at the scale of atoms and subatomic particles, with Einstein's Theory of General Relativity—the modern theory of gravitation as the curvature of space and time. How, he asks, can physicists write equations when the geometry of space itself becomes subject to quantum uncertainty? Quantum gravity, the current frontier in fundamental theory, has proven more difficult to detangle than previous concepts, according to Neiman.
"With the concept of space slipping between our fingers, we seek out alternative footholds on which to base our description of the world," he writes.
This search for alternative footholds is, in essence, a search for a new language to describe reality—and it is the subject of his most recent work, published in the Journal of High Energy Physics. In the paper, Neiman proposes a new vantage point on the geometry of space and time—one that builds on well-established approaches in physics, like holography and twistor theory, to reach new ground.
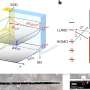
Holography is an offshoot of string theory, the theory that the universe is made up of one-dimensional objects called strings, which was developed in the late 1990s. Holography imagines the ends of the universe as the surface of an infinitely large sphere that forms the boundary of space. Even as geometry fluctuates within this sphere, this "boundary at infinity" on the sphere's surface can remain fixed.

For the past 20 years, holography has been an invaluable tool for conducting quantum-gravity thought experiments. However, astronomical observations have shown that this approach cannot really apply to our world. "The accelerating expansion of our universe and the finite speed of light conspire to limit all possible observations, present or future, to a finite—though very large—region of space," Neiman writes.
In such a world, the boundary at infinity, where the holographic picture of the universe is based, is no longer physically meaningful. A new frame of reference may be needed—one that does not attempt to find a fixed surface in space, but which leaves space behind altogether.
In the 1960s, in an attempt to understand quantum gravity, physicist Roger Penrose proposed such a radical alternative. In Penrose's twistor theory, geometric points are replaced by twistors—entities that most closely resemble stretched, light ray-like shapes. Within this twistor space, Penrose discovered a highly efficient way to represent fields that travel at the speed of light, such as electromagnetic and gravitational fields. Reality, however, is composed of more than fields—any theory needs also to account for the interactions between fields, such as the electric force between charges, or, in the more complicated case of General Relativity, gravitational attraction resulting from the energy of the field itself. However, including the interactions of General Relativity into this picture has proven a formidable task.
So can we express in twistor language a full-fledged quantum gravitational theory, perhaps simpler than General Relativity, but with both fields and interactions fully taken into account? Yes, according to Neiman.
Neiman's model builds on higher spin gravity, a model developed by Mikhail Vasiliev in the 1980s and '90s. Higher spin gravity can be thought of as the "smaller cousin" of String Theory, "too simple to reproduce General Relativity, but very instructive as a playground for ideas," as Neiman puts it. In particular, it is perfectly suited for exploring possible bridges between holography and twistor theory.
On one hand, as discovered by Igor Klebanov and Alexander Polyakov in 2001, higher spin gravity, just like string theory, can be described holographically. Its behavior within space can be captured completely in terms of a boundary at infinity. On the other hand, its equations contain twistor-like variables, even if these are still tied to particular points in ordinary space.
From these starting points, Neiman's paper takes an additional step, constructing a mathematical dictionary that ties together the languages of holography and twistor theory.
"The underlying math that makes this story tick is all about square roots," writes Neiman. "It's about identifying subtle ways in which a geometric operation, such as a rotation or reflection, can be done 'halfway.' A clever square root is like finding a crack in a solid wall, opening it in two, and revealing a new world."
Using square roots in this way has a longstanding history in math and physics. In fact, the intrinsic shape of all matter particles—such as electrons and quarks—as well as twistors, is described by a square root of ordinary directions in space. In a subtle technical sense, Neiman's method for connecting space, its boundary at infinity, and twistor space, boils down to taking such a square root again.
Neiman hopes that his proof of concept can pave the way toward a quantum theory of gravity that does not rely on a boundary at infinity.
"It will take a lot of creativity to uncover the code of the world," says Neiman. "And there's joy in fumbling around for it."
More information: Yasha Neiman, The holographic dual of the Penrose transform, Journal of High Energy Physics (2018). DOI: 10.1007/JHEP01(2018)100
Provided by Okinawa Institute of Science and Technology