Army's brain-like computers moving closer to cracking codes
U.S. Army Research Laboratory scientists have discovered a way to leverage emerging brain-like computer architectures for an age-old number-theoretic problem known as integer factorization.
By mimicking the brain functions of mammals in computing, Army scientists are opening up a new solution space that moves away from traditional computing architectures and towards devices that are able to operate within extreme size-, weight-, and power-constrained environments.
"With more computing power in the battlefield, we can process information and solve computationally-hard problems quicker," said Dr. John V. "Vinnie" Monaco, an ARL computer scientist. "Programming the type of devices that fit these criteria, for example, brain-inspired computers, is challenging, and cracking crypto codes is just one application that shows we know how to do this."
The problem itself can be stated in simple terms. Take a composite integer N and express it as the product of its prime components. Most people have completed this task at some point in grade school, often an exercise in elementary arithmetic. For example, 55 can be expressed as 5*11 and 63 as 3*3*7. What many didn't realize is they were performing a task that if completed quickly enough for large numbers, could break much of the modern day internet.
Public key encryption is a method of secure communication used widely today, based on the RSA algorithm developed by Rivest, Shamir, and Adleman in 1978. The security of the RSA algorithm relies on the difficulty of factoring a large composite integer N, the public key, which is distributed by the receiver to anyone who wants to send an encrypted message. If N can be factored into its prime components, then the private key, needed to decrypt the message, can be recovered. However, the difficulty in factoring large integers quickly becomes apparent.
As the size of N increases by a single digit, the time it would take to factor N by trying all possible combinations of prime factors is approximately doubled. This means that if a number with ten digits takes 1 minute to factor, a number with twenty digits will take about 17 hours and a number with 30 digits about two years, an exponential growth in effort. This difficulty underlies the security of the RSA algorithm.
Challenging this, Monaco and his colleague Dr. Manuel Vindiola, of the lab's Computational Sciences Division, demonstrated how brain-like computers lend a speedup to the currently best known algorithms for factoring integers.
The team of researchers have devised a way to factor large composite integers by harnessing the massive parallelism of novel computer architectures that mimic the functioning of the mammalian brain. So called neuromorphic computers operate under vastly different principles than conventional computers, such as laptops and mobile devices, all based on an architecture described by John von Neumann in 1945.
In the von Neumann architecture, memory is separate from the central processing unit, or CPU, which must read and write to memory over a bus. This bus has a limited bandwidth, and much of the time, the CPU is waiting to access memory, often referred to as the von Neumann bottleneck.
Neuromorphic computers, on the other hand, do not suffer from a von Neumann bottleneck. There is no CPU, memory, or bus. Instead, they incorporate many individual computation units, much like neurons in the brain.

These units are connected by physical or simulated pathways for passing data around, analogous to synaptic connections between neurons. Many neuromorphic devices operate based on the physical response properties of the underlying material, such as graphene lasers or magnetic tunnel junctions. Because of this, these devices consume orders of magnitude less energy than their von Neumann counterparts and can operate on a molecular time scale. As such, any algorithm capable of running on these devices stands to benefit from their capabilities.
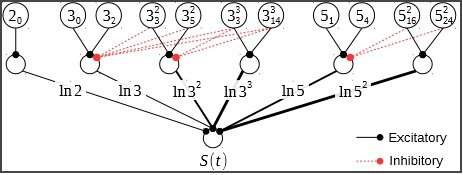
The speedup acquired by the ARL researchers is due to the formulation of a method for integer factorization with the help of a neuromorphic co-processor. The current fastest algorithms for factoring integers consist primarily of two stages, sieving and a matrix reduction, and the sieving stage comprises most of the computational effort.
Sieving involves searching for many integers that satisfy a certain property called B-smooth, integers that don't contain a prime factor greater than B. Monaco and Vindiola were able to construct a neural network that discovers B-smooth numbers quicker and with greater accuracy than on a von Neumann architecture. Their algorithm leverages the massive parallelism of brain-inspired computers and the innate ability of individual neurons to perform arithmetic operations, such as addition. As neuromorphic architectures continue to increase in size and speed, not limited by Moore's Law, their ability to tackle larger integer factorization problems also grows. In their work, it's estimated that 1024-bit keys could be broken in about a year, a task once thought to be out of reach. For comparison, the current record, a 232 decimal digit number (RSA-768) took about 2,000 years of computing time over the course of several years.
From a broader perspective, this discovery pushes us to question how a shift in computing paradigm might affect some of our most basic security assumptions. As emerging devices shift to incorporate massive parallelism and harness material physics to compute, the computational hardness underlying some security protocols may be challenged in ways not previously imagined. This work also opens the door to new research areas of emerging computer architectures, in terms of algorithm design and function representation, alongside low-power machine learning and artificial intelligence applications.
"Encrypted messages in warfare often have an expiration date, when their contents become un-actionable," Monaco said. "There is an urgency to decrypt enemy communications, especially those at the field level, since these expire the quickest, compared to communication at higher echelons. In field conditions, power and connectivity are extremely limited. This is a strong motivating factor for using a brain-inspired computer for such a task where conventional computers are not practical."
More information: John V. Monaco et al, Factoring Integers With a Brain-Inspired Computer, IEEE Transactions on Circuits and Systems I: Regular Papers (2017). DOI: 10.1109/TCSI.2017.2771533
John V. Monaco et al. Integer factorization with a neuromorphic sieve, 2017 IEEE International Symposium on Circuits and Systems (ISCAS) (2017). DOI: 10.1109/ISCAS.2017.8050978
Provided by U.S. Army Research Laboratory