Statisticians develop efficient method for comparing multi-group, high-dimensional data
MANOVA (multivariate analysis of variance) is a commonly used statistical method in data analysis to determine if there is any difference in the means of different groups of data. However, the classical approach is not suitable for analysing high-dimensional data. High-dimensional data often make the traditional MANOVA methods invalid since in a traditional MANOVA, the dimension is assumed to be fixed and has to be much smaller than the number of observations. In a high-dimensional MANOVA setting, this is no longer true. Prof ZHANG Jin-Ting from the Department of Statistics and Applied Probability, NUS and his Ph.D. students have developed a new high-dimensional MANOVA method which can be used to compare the means of several data groups involving high-dimensional data efficiently.
The new method relaxes many mathematical conditions and restrictions imposed in the literature. One of them is the homoscedasticity assumption. This assumption is a mathematical condition which requires that the data of different groups to have the same variation patterns. Their new method also resolves the computational issues involved in the practical implementation of MANOVA for high-dimensional data. It does this by utilising computationally efficient high-level matrix calculations.
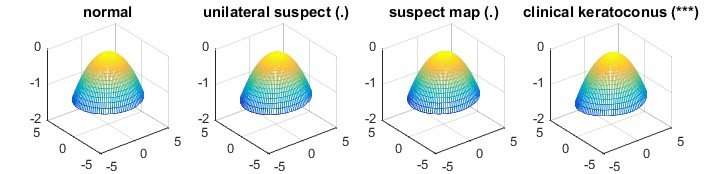
Although it is widely applicable and performs well for many real life datasets, the proposed method may be less effective in certain situations because the variation and correlation information of variables is not fully used. When analysing corneal surface data (see figure below), the associated covariance matrix which contains the variation and correlation information from the data is computed. If the number of corneal surfaces is larger than the number of measurements of a corneal surface, the computed covariance matrix is invertible, meaning that the test statistic can be obtained using the traditional MANOVA test. In a high-dimensional setting, this is not possible as the number of corneal surfaces (150 = 43+14+21+72 samples) is much smaller than the number of measurements (6,912 dimensions). However, the variation and correlation information is still partially used in estimating the parameters of the test statistic. Prof Zhang and his research team are studying this to develop better statistical methods which can handle such situations.
More information: Bu Zhou et al. High-dimensional general linear hypothesis testing under heteroscedasticity, Journal of Statistical Planning and Inference (2017). DOI: 10.1016/j.jspi.2017.03.005
Jin-Ting Zhang et al. Linear hypothesis testing in high-dimensional one-way MANOVA, Journal of Multivariate Analysis (2017). DOI: 10.1016/j.jmva.2017.01.002
Provided by National University of Singapore