Scientists discover more than 600 new periodic orbits of the famous three-body problem
The famous three-body problem can be traced back to Isaac Newton in 1680s. Studies on the three-body problem led to the discovery of the so-called sensitivity dependence of initial condition (SDIC) of chaotic dynamic systems. Today, chaotic dynamics are widely regarded as the third great scientific revolution in physics in 20th century, comparable to relativity and quantum mechanics. Thus, studies on the three-body problem have very important scientific significance.
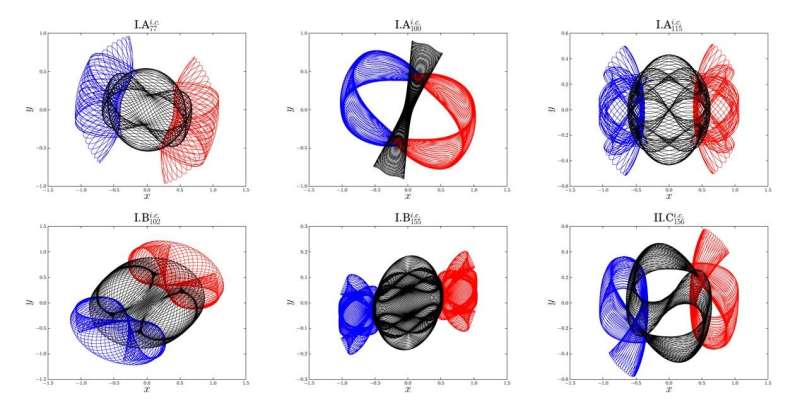
In 1890, Poincare determined that trajectories of three-body systems are commonly non-periodic, i.e. not repeating. This can explain why it is so hard to obtain the periodic orbits of three-body systems. In the 300 years since the three-body problem was first recognized, only three families of periodic orbits had been found. In 2013, Suvakov and Dmitrasinovic [Phys. Rev. Lett. 110, 114301 (2013)] made a breakthrough, finding 13 new distinct periodic orbits belonging to 11 new families of the Newtonian planar three-body problem with equal mass and zero angular momentum. Now, two scientists, XiaoMing Li and ShiJun Liao at Shanghai Jiaotong University, China, have successfully determined 695 families of periodic orbits of the same Newtonian planar three-body system using the TH-2 supercomputer at Guangzhou, China. Their results have been published in SCIENCE CHINA-Physics Mechanics & Astronomy. Videos of these orbits are available here.
These 695 periodic orbits include the well-known figure-eight family found by Moore in 1993, the 11 families found by Suvakov and Dmitrasinovic in 2013, and more than 600 new families reported for the first time. The two scientists used the so-called clean numerical simulation (CNS), a new numerical strategy for reliable simulations of chaotic dynamic systems proposed by the second author in 2009, which is based on a high order of Taylor series and multiple precision data, plus a convergence/reliability check. The CNS can reduce truncation errors and round-off errors so effectively that numerical noise is negligible over a long enough interval of time, thus more periodic orbits of the three-body system can be obtained.
As reported by Montgomery in 1998, each periodic orbit in real space of the three-body system corresponds to a closed curve on the so-called "shape sphere," which is characterized by its topology using the so-called "free group element." The averaged period of an orbit is equal to the period of the orbit divided by the length of the corresponding free group element. These 695 families suggest that the square of the average period times the cube of the total kinetic and potential energy is approximately equal to a constant. The generalized Kepler's third law reveals that the three-body system has something in common that might deepen the understanding of three-body system.
According to the scientists, the discovery of the more than 600 new periodic orbits is mainly due to the advance in computer science and the use of the new strategy of numerical simulation for chaotic dynamic systems, namely the CNS. It should be emphasized that 243 more new periodic orbits of the three-body system are found by means of the CNS. In other words, if traditional algorithms with double precision were used, about 40 percent of the new periodic orbits would be lost. This indicates the novelty and originality of the CNS, since any new methods must offer something novel.
More information: XiaoMing Li et al, More than six hundred new families of Newtonian periodic planar collisionless three-body orbits, Science China Physics, Mechanics & Astronomy (2017). DOI: 10.1007/s11433-017-9078-5
Journal information: Physical Review Letters
Provided by Science China Press