Wriggling microtubules help understand coupling of 'active' defects and curvature
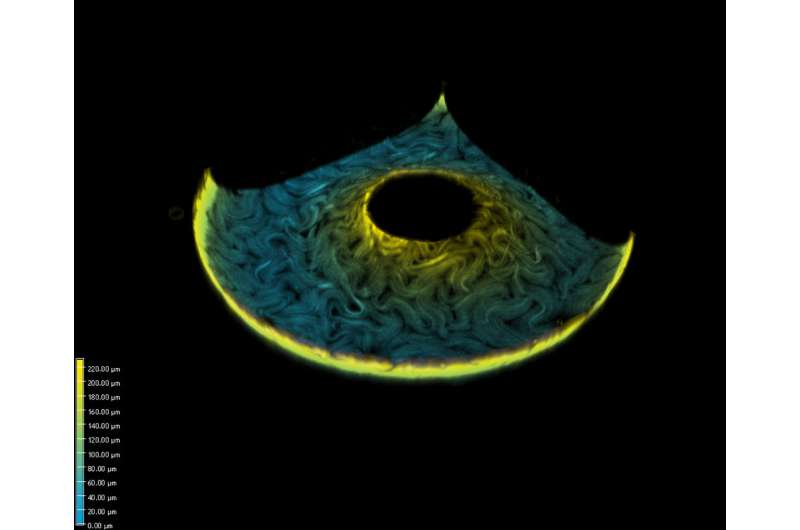
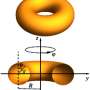
Imagine a tiny donut-shaped droplet, covered with wriggling worms. The worms are packed so tightly together that they must locally line up with respect to each other. In this situation, we would say the worms form a nematic liquid crystal, an ordered phase similar to the materials used in many flat panel displays.
However, the nematic phase formed by the worms is filled with tiny regions where the local alignment is lost - defects in the otherwise aligned material. In addition, because the worms are constantly moving and changing their configuration, this nematic phase is active and far from equilibrium.
In research reported in the journal Nature Physics, scientists from the Georgia Institute of Technology and Leiden University in The Netherlands have described the results of a combined theoretical and experimental examination of such an active nematic on the surface of donut-shaped - toroidal - droplets. However, the researchers didn't use actual worms, but an active nematic composed of flexible filaments covered with microscopic engines that are constantly converting energy into motion.
This particular active material, originally developed at Brandeis University, borrows elements of cellular machinery, with bundles of rod-like microtubules forming the filaments, kinesin motor proteins acting as the engines, and ATP as the fuel. When this activity is combined with defects, the defects "come to life," moving around like swimming microorganisms and exploring space - in this case, exploring the surface of the toroidal droplets.
By studying toroidal droplets covered by this active nematic, the researchers confirmed a longstanding theoretical prediction about liquid crystals at equilibrium, first discussed by Bowick, Nelson and Travesset [Phys.Rev. E 69, 041102 (2004)] that nematic defects on the curved surface of such droplets will be sensitive to the local curvature. However, since the active nematic used in this work is far from equilibrium, the researchers also found how the internal activity changed and enriched the expectations.
"There have been predictions that say defects are very sensitive to the space they inhabit, specifically to the curvature of the space," said Perry Ellis, a graduate student in the Georgia Tech School of Physics and the paper's first author. "The torus is a great place to investigate this because the outside of the torus, the part that looks locally like a sphere, has positive curvature while the inner part of a torus, the part that looks like a saddle, has negative curvature."
"The quantity that characterizes a defect is what we call its topological charge or winding number," said Alberto Fernandez-Nieves, a professor in Georgia Tech's School of Physics and another of the paper's co-authors. "It expresses how the alignment direction of the nematic liquid crystal changes as we go around the defect. This topological charge is quantized, meaning that it can only take values from a discrete set that are multiples of one-half. "
In these experiments, each defect has a topological charge of +1/2 or -1/2. To determine the charge and location of every defect, Ellis observed the toroidal droplets over time using a confocal microscope and then analyzed the resulting video using techniques borrowed from computer vision. The researchers found that even with the molecular motors driving the system out of equilibrium, the defects were still able to sense the curvature, with the +1/2 defects migrating towards the region of positive curvature and the -1/2 defects migrating towards the region of negative curvature.
In this new work, the scientists took a step forward in understanding how to control and guide defects in an ordered material.
"We have learned that we can control and guide partially ordered active matter using the curvature of the underlying substrate," said Fernandez-Nieves. "This work opens opportunities to study how the defects in these materials arrange on surfaces that do not have constant curvature. This opens the door for controlling active matter using curvature."
An unexpected finding of the study was that the constant motion of the defects causes the average topological charge to become continuous, no longer taking only values that are multiples of one-half.
"In the active limit of our experiments, we found that the topological charge becomes a continuous variable that can now take on any value," said Fernandez-Nieves. "This is reminiscent of what happens to many quantum systems at high temperature, where the quantum, discrete nature of the accessible states and associated variables is lost.
Instead of being characterized by quantized properties, the system becomes characterized by continuum properties."
Ellis' observations of the droplets compared well with those of numerical simulations done by Assistant Professor Luca Giomi and postdoctoral researcher Daniel Pearce at the Instituut-Lorentz for Theoretical Physics at the Universiteit Leiden in The Netherlands.
"Our theoretical model helped us decipher the experimental results and fully understand the physical mechanism governing defect motion," said Pearce, "but also allowed us to go beyond the current experimental evidence." Added Giomi: "Activity changes the nature of the interaction between defects and curvature. In weakly active systems, defects are attracted by regions of like-sign Gaussian curvature. But in strongly active systems, this effect becomes less relevant and defects behave as persistent random-walkers confined in a closed and inhomogeneous space".
There are many examples of active systems driven by internal activity, including swimming microorganisms, bird flocks, robot swarms and traffic flows. "Active materials are everywhere, so our results aren't limited to just this system on a torus," Ellis added. "You could see the same behavior in any active system with defects."
The research sets the stage for future work in active fluids. "Our results introduce a new framework to explore the mechanical properties of active fluids and suggest that partially ordered active matter can be guided and controlled via gradients in the intrinsic geometry of the underlying substrate," the authors wrote in a summary of their paper.
More information: Perry W. Ellis et al, Curvature-induced defect unbinding and dynamics in active nematic toroids, Nature Physics (2017). DOI: 10.1038/nphys4276
Journal information: Nature Physics
Provided by Georgia Institute of Technology