Localized orbital scaling correction functional ushering DFT to a new level of accuracy
Kohn-Sham density functional theory is one of the most successful theories in chemistry. It is formally rigorous; its relatively low computational cost and competitive accuracy in small and medium-sized systems make it one of the most popular methods in electronic structure calculations, and perhaps the only choice for modeling quantum effects of electrons in large chemical and biological systems. Nevertheless, the exact functional is not explicitly known and the state-of-the-art density functional approximations (DFAs) suffer from systematic errors. One of the dominant errors in DFAs is the delocalization error, which is ubiquitous and manifested in various ways. This has been a challenging open problem for decades. Recently, Chen Li, Neil Qiang Su and Weitao Yang from Duke University and Xiao Zheng from the University of Science and Technology of China developed a novel localized orbital scaling correction (LOSC) framework that demonstrates systematic elimination of the delocalization error.
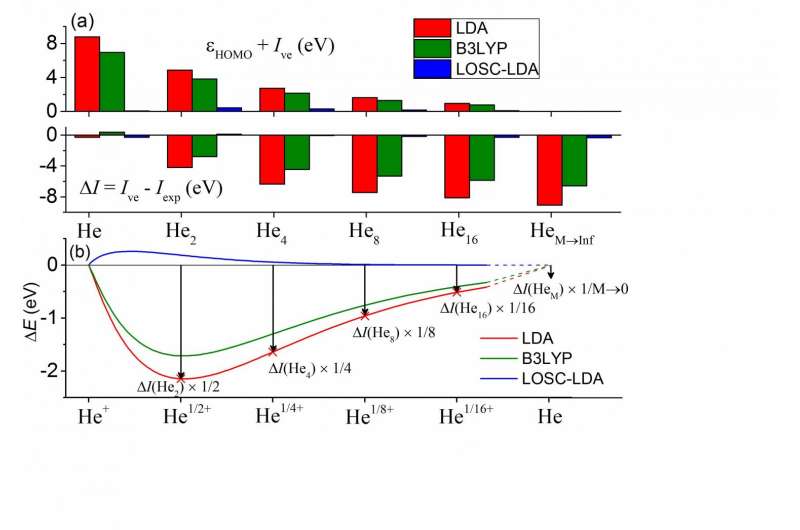
The major consequences of delocalization errors in DFAs can be categorized in two aspects: (1) Kohn-Sham (KS) orbital energy error and (2) total energy error. The delocalization error leads to important failures in practical applications such as the unphysical underestimation of band gaps, the excessively delocalized electron distributions and wrong charge transfers. Regarding these two aspects of errors, both are manifested in a size-dependent manner. In particular, among the KS orbital energies, the highest occupied molecular orbital (HOMO) energy, εHOMO, is supposed to agree with the (negative) vertical ionization potential (-Ive), as required by the exact functional. Furthermore, the Ive as calculated by DFAs are supposed to agree with the experimental value, Iexp.
For commonly used DFAs, the two conditions are not satisfied. As shown by the helium cluster calculations in the subfigure (a), the HOMO energy by the local density approximation (LDA) shows a positive error compared to -Ive while Ive exhibits a negative error, and the two errors are displayed in a size-dependent manner, suggesting that the delocalization error of DFAs has to show up in one way or the other, or both, while the sum of the magnitudes remains unchanged. Moreover, this is prevalent in all kinds of DFAs, including the most popular B3LYP functional, as shown in green.
To understand these errors, chemists can map them into the errors of a fractionally charged He atom, as illustrated in the subfigure (b). The fractional system energies are supposed to scale linearly with the fractional electron number n (0?n<1) for the exact functional. Shown in subfigure (b) is the energy deviation from the linearity condition for a single He atom, where the fractional system energies are underestimated- this defines the delocalization error. Moreover, the fractional charge error in (b) has 1-1 correspondence with the total energy error ΔI = Ive - Iexp. In the limit of M goes to infinity, one can deduce that ΔI agrees with the slope error of the E(N) curve at the integer, which is exactly the HOMO energy error of a single He atom. Therefore, all the errors are inter-connected. It is thus possible to eliminate delocalization error systematically through (1) removing the errors in (b) and (2) guaranteeing size-consistent removal of the error in all systems.
In the present work of LOSC, the authors invented novel local variables, called orbitallets, which are localized orbitals (LOs) that achieve locality in both spatial and energy spaces. Through these orbitallets, they were able to express the electron density and KS density matrix in the local representation, where the local occupation matrix composed of fractional numbers arises naturally. Therefore, these local variables are capable of capturing local fractional information precisely and completely in the orbital space, and serve as the perfect building blocks for the LOSC functional. Furthermore, by rewriting the terms in the GSC and LSC functionals in terms of curvature correction formulas and making analogy to the LOSC, they introduced a local curvature matrix, whose elements are designed as a functional of the orbitallets, to be in one-to-one correspondence with the local occupation matrix. Finally, the LOSC formula is written as an explicit and elegant expression over the parent functional in terms of these two matrices.
The LOSC achieves all the desirable features. In the above figure, the LOSC-LDA errors are essentially negligibly small, indicating the validity and size-consistency of the correction. These have also been validated by the much improved dissociation curves of diatomic molecular cations, ranging from H2+, He2+, water dimer cation and benzene dimer cation. The HOMO, LUMO energy errors have been much reduced and the good performance maintains as system size grows. This has been demonstrated by tests on polyacene and trans-polyacetylene oligomers. Furthermore, the LOSC is capable of retrieving the right electron density when the parent DFAs makes it qualitatively wrong, as shown by the example of a solvated chlorine anion when deprived of an electron.
The performance of LOSC thus shows promise of eliminating delocalization error systematically within the KS density functionals. It is worth noticing that unlike traditional paradigm of designing functionals using the density, the density gradients, the kinetic energy density, etc., the LOSC framework involves completely new ingredients, the orbitallets, which themselves are implicit functionals of the KS density matrix, and demonstrated their unique capability of addressing longstanding problems associated with traditional DFAs. This reflects a paradigm change in designing functionals, and greatly broadens the way in the exploration for the exact functional in its own living space. In this sense, LOSC has ushered the trend in developing new generation of density functional approximations, promoting density functional theory to a new level of accuracy.
More information: Chen Li et al, Localized Orbital Scaling Correction for Systematic Elimination of Delocalization Error in Density Functional Approximations, National Science Review (2017). DOI: 10.1093/nsr/nwx111
Provided by Science China Press