Placing buildings in a landscape with computational mathematics
A research project within the Building Futures Area of Advance at Chalmers is investigating how to model and compute wind and view by using computational mathematics in order to find suitable sites on which to position buildings.
Carl Lundholm has been a Doctoral Student in Computational Mathematics in the Mathematical Sciences Department since August 2015. Together with his supervisor, Anders Logg, Professor of Computational Mathematics and Profile Leader of Virtual Cities within Building Futures, he is conducting research into finite element methods on overlapping meshes. Working with the architecture firm CREAM Architects and the University of Gothenburg, they are looking into how this research can be used to find suitable sites on which to position buildings in the landscape. This is taking place within the project titled: Computational Design of Settlement Layouts.
What is an overlapping mesh?
Mesh refers to the computational mesh obtained from a space discretisation. Space discretisation means that an area is divided up into smaller sections, for example like a chessboard. In this context, overlapping meshes means that a small mesh is generated around each building, which is then placed into a larger mesh that has been generated around the landscape.
What are the advantages of overlapping meshes?
The idea is to quickly and easily be able to test various settlement configurations by moving the smaller house meshes in the static landscape mesh. This means that computationally costly mesh generation is only initially required in contrast to the classic method of using a single mesh that would need to be re-generated when a building is moved.
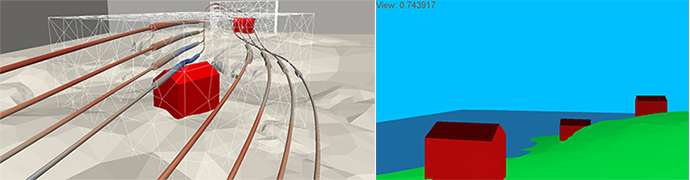
What are the criteria for positioning buildings?
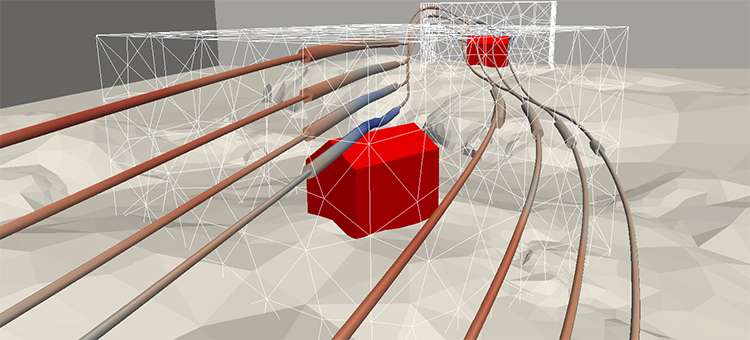
The suitability of a site has until now been determined by two factors: wind (flow) around and view from the building. In order to model flow, a finite element method for Stokes equations on overlapping meshes has been used. The model for the view from the building is based on a measure of view that has been created specially for the project, as well as rasterization. With a given position and direction, the view measure produces a value between zero and one, where the higher value represents a better view. FEniCS software, with its new multimesh functionality, has been used for implementation and computation. Figure 1 illustrates some of the simulation results from the models for flow and view. The main challenges in the project are currently the task of making the software more robust and faster.
More information: Simulation of flow and view with applications in computational design of settlement layouts. arxiv.org/abs/1610.02277
Provided by Chalmers University of Technology