Researchers create a new type of computer that can solve problems that are a challenge for traditional computers

The processing power of standard computers is likely to reach its maximum in the next 10 to 25 years. Even at this maximum power, traditional computers won't be able to handle a particular class of problem that involves combining variables to come up with many possible answers, and looking for the best solution.
Now, an entirely new type of computer that blends optical and electrical processing, reported Oct. 20 in the journal Science, could get around this impending processing constraint and solve those problems. If it can be scaled up, this non-traditional computer could save costs by finding more optimal solutions to problems that have an incredibly high number of possible solutions.
"This is a machine that's in a sense the first in its class, and the idea is that it opens up a sub-field of research in the area of non-traditional computing machines," said Peter McMahon, postdoctoral scholar in applied physics and co-author of the paper. "There are many, many questions that this development raises and we expect that over the next few years, several groups are going to be investigating this class of machine and looking into how this approach will pan out."
The traveling salesman problem
There is a special type of problem - called a combinatorial optimization problem - that traditional computers find difficult to solve, even approximately. An example is what's known as the "traveling salesman" problem, wherein a salesman has to visit a specific set of cities, each only once, and return to the first city, and the salesman wants to take the most efficient route possible. This problem may seem simple but the number of possible routes increases extremely rapidly as cities are added, and this underlies why the problem is difficult to solve.
"Those problems are challenging for standard computers, even supercomputers, because as the size grows, at some point, it takes the age of the universe to search through all the possible solutions," said Alireza Marandi, a former postdoctoral scholar at Stanford and co-author of the study. "This is true even with a supercomputer because the growth in possibilities is so fast."
It may be tempting to simply give up on the traveling salesman, but solving such hard optimization problems could have enormous impact in a wide range of areas. Examples include finding the optimal path for delivery trucks, minimizing interference in wireless networks, and determining how proteins fold. Even small improvements in some of these areas could result in massive monetary savings, which is why some scientists have spent their careers creating algorithms that produce very good approximate solutions to this type of problem.
An Ising machine
The Stanford team has built what's called an Ising machine, named for a mathematical model of magnetism. The machine acts like a reprogrammable network of artificial magnets where each magnet only points up or down and, like a real magnetic system, it is expected to tend toward operating at low energy.
The theory is that, if the connections among a network of magnets can be programmed to represent the problem at hand, once they settle on the optimal, low-energy directions they should face, the solution can be derived from their final state. In the case of the traveling salesman, each artificial magnet in the Ising machine represents the position of a city in a particular path.
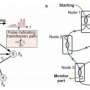
Rather than using magnets on a grid, the Stanford team used a special kind of laser system, known as a degenerate optical parametric oscillator, that, when turned on, will represent an upward- or downward-pointing "spin." Pulses of the laser represent a city's position in a path the salesman could take. In an earlier version of this machine (published two years ago), the team members extracted a small portion of each pulse, delayed it and added a controlled amount of that portion to the subsequent pulses. In traveling salesman terms, this is how they program the machine with the connections and distances between the cities. The pulse-to-pulse couplings constitute the programming of the problem. Then the machine is turned on to try to find a solution, which can be obtained by measuring the final output phases of the pulses.
The problem in this previous approach was connecting large numbers of pulses in arbitrarily complex ways. It was doable but required an added controllable optical delay for each pulse, which was costly and difficult to implement.
Scaling up
The latest Stanford Ising machine shows that a drastically more affordable and practical version could be made by replacing the controllable optical delays with a digital electronic circuit. The circuit emulates the optical connections among the pulses in order to program the problem and the laser system still solves it.
Nearly all of the materials used to make this machine are off-the-shelf elements that are already used for telecommunications. That, in combination with the simplicity of the programming, makes it easy to scale up. Stanford's machine is currently able to solve 100-variable problems with any arbitrary set of connections between variables, and it has been tested on thousands of scenarios.
A group at NTT in Japan that consulted with Stanford's team has also created an independent version of the machine; its study has been published alongside Stanford's by Science. For now, the Ising machine still falls short of beating the processing power of traditional digital computers when it comes to combinatorial optimization. But it is gaining ground fast and the researchers are looking forward to seeing what other work will be possible based on this breakthrough.
"I think it's an exciting avenue of exploration for finding alternative computers. It can get us closer to more efficient ways of tackling some of the most daunting computational problems we have," said Marandi. "So far, we've made a laser-based computer that can target some of these problems, and we have already shown some promising results."
More information: A fully-programmable 100-spin coherent Ising machine with all-to-all connections, Science, DOI: 10.1126/science.aah5178 , science.sciencemag.org/content … 0/19/science.aah5178
Journal information: Science
Provided by Stanford University