Experimental test verifies Heisenberg's measurement uncertainty principle

(Phys.org)—Werner Heisenberg originally proposed the uncertainty principle in 1927, but his original proposal was somewhat different than how it is interpreted today. As a recent paper in Physical Review Letters explains, Heisenberg's original statement was about error and disturbance in a measurement process. Over the years, however, Heisenberg's original proposal has been restated in terms of the uncertainties intrinsic to quantum states. This aspect of the uncertainty principle has been studied extensively with well-developed theories and verified experimentally.

On the other hand, Heisenberg's original proposal regarding error in the measurement process is not as well understood. In the new paper, a team of researchers led by Professor Jiangfeng Du at the University of Science and Technology of China has reported an experimental test of the measurement aspect of Heisenberg's uncertainty principle using nuclear-spin qubits.

In his original proposal, Heisenberg predicted a tradeoff between error and disturbance. He suggested that when a gamma-ray microscope measures the position of an electron, the measurement inevitably disturbs the electron's momentum. The smaller the measurement error, the larger the disturbance, and vice versa. This idea was described qualitatively but a complete quantitative description is still lacking today.

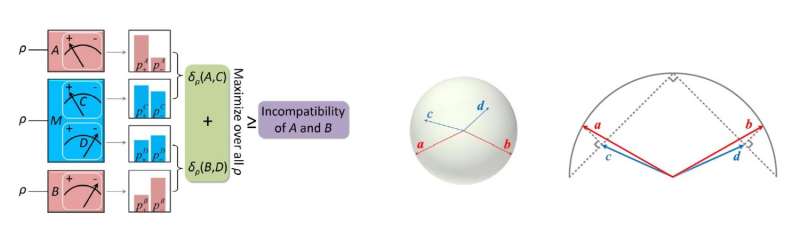
In the new experiment, the researchers have verified a related tradeoff that builds on a recent proposal. In this tradeoff, measurement inaccuracies are quantified geometrically.

"In recent years, the quantification of Heisenberg's original idea has drawn lots of attention, and a number of experiments have been performed," Du told Phys.org. "However, the physical validity of some parts of the theory is in dispute. A few years ago, Busch, Lahti, and Werner proposed an innovative approach which is more sensible and persuasive. Our work is based on Busch, Lahti, and Werner's theory, and makes some improvement. We reformulated their theoretical framework and derived a new tradeoff relation which was verified by our experiment. In this sense, our work tests a fundamental aspect of quantum physics."

In order to verify the new tradeoff, the researchers had to approach the situation somewhat indirectly. According to the measurement uncertainty principle, incompatible observables, such as position and momentum, cannot be measured simultaneously. So instead, the researchers simultaneously measured two compatible observables that are designed to approximate two incompatible observables. Compatible observables can be measured simultaneously, and simulate the measurement device that introduces error and disturbance.

As expected, the experimental results verify the tradeoff, showing that the worst-case inaccuracy is determined by the incompatibility of the observables. Overall, the work provides a deeper understanding of Heisenberg's original idea about the uncertainty principle, and could also have practical applications.

"In the future, we may consider the implications for the area of quantum information technology," Du said.

© 2016 Phys.org